A Survey of Basic Voting Methods

Given a field of candidates running in an election for the same position, a single winner method will select only one. Choosing a governor would be an example of this; if there can only be one governor of a state, then the governor must be decided by a single-winner method. A multiple winner method will select more than one candidate, for example an election that fills ten seats in a legislature, with one electorate choosing from a field of ninety candidates.

I.A. Non-ranked ballot systems

I.A.1. Plurality

Plurality is the most common single winner method used in the world today. The plurality method simply gives the victory to the candidate who receives the most votes (a plurality). This may sound intuitive, but unfortunately it has severe flaws. The problems stem from the difference between a plurality and a majority.

Example 1: One candidate from the far right receives 20% of the vote, and eight candidates from the left receive 7%, 9%, 10%, 10%, 10%, 10%, 11%, and 13% of the vote. The right winger will win a plurality election, despite the fact that 80% of the voters preferred a leftist candidate.

It is believed that on average there will only be two viable candidates for any given election under the plurality system. This is because rather than picking the candidate who is their sincere favorite, most voters are likely to instead vote for the one of the perceived front-runners whom they prefer, since this is the best chance they have of their vote making a positive difference. This tendency is known as Duverger's law[*], and is thought to be the primary cause of two-party systems where they exist.

Given the existence of two major party candidates who dominate an election field together, the entrance of a new candidate is most likely to split the vote of the major party candidate whom they have the most in common with, thus giving the other candidate an advantage, and going directly against the wills of would-be supporters of the emergent candidate. This 'spoiler effect' is an extremely strong deterrent against new parties and candidates entering a race where a close competition has already been established between two major parties. This is a fatal problem for the competitiveness of political races and the accountability of politicians. Standards are very low for political candidates because they only need to be preferred over a single other viable candidate, rather than over a large field of viable candidates. This dynamic also encourages negative campaigning, and severely limits the range of political discourse.

Criteria summary for plurality

Criteria passed: majority, monotonicity, participation, consistency, Pareto, later preferences

Criteria failed: mutual majority, Condorcet, Condorcet loser, Smith, independence of clones

Strategic vulnerability: Very strong and very damaging compromising-reversal incentive.

I.A.2. Two round runoff

The second most common single-winner method is the two round runoff. The rules for two round runoff vary slightly, but the most common procedure is this: An initial election is held, and if any candidate gets a majority of the votes, she is declared the winner. If not, then a second election is held between the two candidates who received the most votes in the first election. This assures that the resulting winner is preferred by a majority to at least the one other candidate who makes it to the second election.

In example 1, a second election would be held between the right wing candidate with 20% and the leftist candidate with 13% of the initial vote. Since an 80% majority of the voters preferred leftist candidates, the remaining leftist would be likely to win with ease.

Of course, by the same logic as above, it is not certain that the candidate with 13% is the best representative of the leftists. This is the basic limitation of the two round runoff’s effectiveness.

Criteria summary for two round runoff:

Criteria passed: majority, later preferences, Pareto, Condorcet loser

Criteria failed: mutual majority, Condorcet, Smith, participation, consistency, monotonicity

Strategic vulnerability: There is a somewhat strong and potentially quite damaging compromising-reversal incentive. There is some vulnerability to paradoxical strategies. There is no burying vulnerability.

I.A.3. Approval voting

In approval voting, you can vote only once for each candidate, but you may vote for as many candidates as you like. The winner is the candidate with the most votes. For example, if A, B, C, D, and E are running in an election, you can vote only for A, you can vote for A and B, or you can vote for A, B, and C. You could vote for all five of the candidates if you like, but doing so is essentially equivalent to not voting at all, since your vote affects all the candidates equally.

Approval voting is probably an unambiguous improvement over plurality. For one thing, where plurality often forces people to choose between voting for a candidate whom they perceive to be viable and a candidate whom they strongly agree with, approval allows people to do both. Thus, it arguably gives candidates a fair chance to prove themselves on election day even if they are not expected to be one of the top two contenders. Some also argue that approval would do fairly well at choosing strong compromise candidates. They make an interesting case, but I would like to see this happen in practice before I accept it as being true.

Approval does have significant limitations. Take example 1.1, a race between a Conservative party candidate, a Labor party candidate, and a Democratic party candidate. 45% of the voters prefer the Conservative candidate over both the Democratic candidate and the Labor party candidate, and will only approve him. 30% of the voters prefer the Labor candidate as their first choice, but strongly prefer the Democratic candidate over the Conservative candidate. 25% of the voters prefer the Democratic candidate as their first choice, but strongly prefer the Labor candidate over the Conservative candidate.

This information can be summarized in handy ways, as below. The notation “30%: Labor > Democrat > Conservative” means that 30% of the voters would prefer the Democrat to the Labor candidate, and the Labor candidate to the conservative candidate. The notation “45%: Conservative > Labor = Democrat” means that 45% of the voters most prefer the Conservative candidate, and consider the remaining candidates to be roughly equal to each other in desirability or undesirability.

45%: Conservative

30%: Labor > Democrat > Conservative

25%: Democrat > Labor > Conservative

Approval voting in itself offers no mechanism to resolve this kind of situation. If the Labor and Democratic voters unite in approving a candidate, then that candidate will beat the Conservative, something that both Labor and Democratic voters want. But which will be the winner, Labor or the Democrats?

If all of the Labor and Democratic voters approve both the Labor and Democratic candidates, then there will be a tie. If all of them except one approves both, and the remaining one only approves the Democrat, then the Democrat will win. If one voter only approves the Democrat, and two only approve Labor, then Labor will win. Thus both Democratic and Labor voters have an incentive to approve only one, but as the numbers grow who follow this incentive, the chances of electing the Conservative increase.

The result is essentially a game of chicken between the Labor and Democratic voters, where approving both candidates is analogous to swerving, approving only their favorite candidate is equivalent to staying on course, and the car crash is the election of the Conservative. It seems that this might cause instability in some cases.

Put another way, the choice between the Labor and Democratic candidates is a relatively haphazard one. Most of the Labor and Democrat voters need to approve both of them in order to beat the Conservative, and most of the Conservative voters won't approve either Labor or Democrat (or else the Conservative won't have a chance), so the choice between L and D is made by a few outliers, or a few people who make a lucky gamble.

The problem is that approval voting only offers voters two levels of support (1 vote, or 0 votes), while the Labor and Democratic voters both have three distinct tiers of preference. What is desirable, then, is a way to give voters a way to express as many levels of support as there are candidates, that is to say, a ranked ballot.

One of the attractive features of approval voting is does not require different voting equipment from plurality voting. In addition, it is very easy to explain. Hence, the cost of switching to approval voting from plurality is very low compared to many other systems which utilize ranked ballots and have more complex rules. However, there may be many situations where this added cost is more than compensated for by the more sophisticated communication from voters to government that is made possible by some ranked ballot methods.

In general, I feel that it is difficult to accurately predict how approval voting will play out in practice, since we cannot map preferences directly onto votes, and we rely on our own understanding of rather subtle dynamics of voter psychology, voter interaction, voter strategy. It will be very interesting for approval to be tried on larger scales, to see how it handles more contentious election scenarios. Perhaps approval voting will have a powerfully positive impact on democracy; it's hard to know at this point. However, it does seem clear that it has substantial advantages to plurality with few disadvantages, so in my opinion it is probably worth supporting as an alternative to plurality.

Criteria summary for approval voting

Criteria passed: monotonicity, participation, consistency

Criteria failed: Pareto, majority, mutual majority, Condorcet, Condorcet loser, Smith, independence of clones, later preferences

Strategic vulnerability: "Sincere vote" difficult to define for approval. Compression of preferences forced by the ballot, thus causing similar problems to methods with strong compromising-compression and burying-compression problems.

Note: As it fails the mutual majority criterion (and even the more basic majority criterion), I don't think that approval should be known as a majority rule method. However, there may be some situations where approval voting is preferable to majority rule, especially in electorates that are not very contentious, i.e. where the members are more inclined to seek consensus.

I.B. Ranked ballot methods

Ranked ballot methods allow voters to list the candidates in order of preference, that is first choice, second choice, and so on. Many but not all ranked methods allow voters to give an equal ranking to more than one candidate, for example I can list A as my first choice, B as my second choice, C and D as tied for third, E at fourth, and so on. The standard version of IRV does not allow equal rankings, but all Condorcet versions below do.

In some places, such as Australia, voters are required to rank all of the candidates in order for their ballot to be counted. However, this is not at all necessary from the standpoint of the methods themselves; any ranked system can work from ballots that do not rank everyone, or are ‘truncated’ after a certain point. Generally, ranked ballot methods consider all candidates not ranked on a ballot to be tied for last place.

I.A.1. Borda

Borda is a point count system, where a first choice vote is worth a fixed number of points, a second choice vote is worth a fixed number of points, and so on. The winner is the candidate with the most total points. One common formula for Borda is to make the last place on a ballot be worth zero points, the second to last place worth one point, and so on until the first place, which is worth one less than the number of candidates running. Variations exist which can effect the result of a given election, but the principle remains the same.

Borda is a highly inelegant system that has little merit for use in public elections. For one thing, the strength of a given person's vote is highly variable as it affects the competitions between different candidates. For example, let's say there is a race with two strong frontrunners and some candidates with only a slim chance of winning. If I vote for my own long-odds favorite first, and my preferred compromise candidate second, the strength of my vote as it affects the race between the frontrunners is less than someone else in a similar situation who left their sincere favorite off the ballot. Hence, there are strong and frequent incentives for voters to rank someone other than their sincere favorite in first place. Also, it is extremely common for Borda to offer strong incentives for strategic truncation.

Further weirdnesses abound in the Borda system. For one thing, say that there are two elections with identical ballots cast. The only difference is that in the second election, an extra candidate runs, who is not ranked anywhere on the ballots of any of the voters. Borda is the only system discussed here weird enough that the results of the two elections can be different under these circumstances.

Borda is virtually alone among ranked ballot methods in failing the majority criterion, which states that if a candidate is voted over all other candidates by more than half of the voters, he or she should win.

Borda spectacularly fails the independence of clones criterion, which will be defined later. The basic upshot of this, though, is that it can be a huge advantage for a given constituency to be represented by a large number of candidates in an election, rather than a single candidate or only a few. That is, a constituency can crowd out other constituencies by flooding the election field with similar candidates.

Also, Borda should not be used in multiple-winner elections when proportional representation (which will also be defined later) is appropriate, because it does not produce fully proportional results.

Click here for a more detailed critique of the Borda count.

Criteria summary for the Borda count

Criteria passed: monotonicity, participation, consistency, later preferences, Pareto, Condorcet loser

Criteria failed: majority, mutual majority, Condorcet, Smith, independence of clones

Strategic vulnerability: Strategic vulnerability is a major issue for Borda. Very strong compromising and burying incentives. Also, teaming incentives significantly greater than any other method considered here.

I.A.2. Instant runoff voting / the alternative vote / Hare

This system, called the alternative vote internationally, or sometimes the Hare[*] method or simply 'preference voting', uses a ranked ballot to simulate a process much like a multiple-round runoff election, hence the American name for it, instant runoff voting.

Each ballot is initially assigned to candidates who are listed as the first choice on that ballot. If any candidate already has a majority of the votes at this point, then they automatically win the election. If no one has a majority yet, then the candidate with the fewest top choice votes is eliminated, and the votes cast for them are transferred to the next choice on each ballot. This process continues until one candidate achieves a majority, or until only one candidate remains.

Example 2: The candidates running are “Far Right,” “Right,” “Left,” and “Far Left.”

Again, the notation “5%: A>B>C” means that 5% of the voters indicate A as their first choice, B as their second choice, and C as their third choice. If there are more candidates than A B and C, then they are considered to all be tied for last place on this ballot. (The notation is being used the same way as in example 1.1, except that in that case we were dealing with “internal” voter preferences which couldn’t be expressed on an approval ballot, and now we are dealing with voter preferences as expressed on actual ranked ballots.)

5%: Far Right > Right > Left > Far Left.

40%: Right > Far Right > Left > Far Left

36%: Left > Far Left > Right > Far Right

19%: Far Left > Left > Far Right > Right

The IRV count would go like this:

Far Left Left Right Far Right

19% 36% 40% 5%

round one: nobody has a majority, so Far Right is eliminated, transferring 5% to Right.

+5% 5%

19% 36% 45%

round two: Far Left now has the fewest votes, so she is eliminated, transferring 19% to Left.

~~19%~~ +19%

55% 45%

round three: Left now has a clear majority and wins.

IRV is a step in many of the right directions, as it allows for as many levels of preference as there are candidates, and as a person’s vote retains its full original value after it is transferred. However, it is not perfect, as I will explain in the next section.

Criteria summary for IRV

Criteria passed: majority, mutual majority, later preferences, Pareto, Condorcet loser, independence of clones

Criteria failed: Condorcet, Smith, participation, consistency, monotonicity

Strategic vulnerability: If equal ranking is not allowed, a somewhat strong and potentially quite damaging compromising-reversal incentive. If it is allowed, a relatively less-damaging compromising-compression incentive, along with a reduced compromising-reversal incentive. Because it fails monotonicity, IRV is one of the few methods vulnerable to paradoxical strategies. However, paradoxical strategies in IRV probably tend to be difficult and risky, and the vulnerability is probably not severe.

I.A.3. Condorcet methods

Methods based on the Condorcet[*] principle first use the ranked ballots to ask whether there is any one candidate who would win in a head to head election against every other candidate individually.

To do this, it breaks down the election into a series of pairwise comparisons between every candidate and every other candidate. In a pairwise contest between candidate A and candidate B, a ballot counts as one vote for candidate A if he is ranked above B on that ballot. Also, if candidate A is ranked, and candidate B is not ranked at all on that ballot, then it counts as one vote for candidate A. The position of the other candidates is irrelevant to the pairwise contest between A and B.

If there is one candidate who wins all of their pairwise comparisons (which is more likely than it may sound), then he is a Condorcet winner, and he wins an election with any Condorcet method.

It is possible that there will be no Condorcet winner, for example if A wins her pairwise comparison against B, B wins his pairwise comparison against C, and C wins her pairwise comparison against A. This is called a “majority rule cycle.” There are several methods of breaking cycles, the most interesting of which are described in detail below.

But first some examples where a Condorcet winner does exist. Let’s take example 2 again, an example of a situation where IRV works well.

5%: Far Right > Right > Left > Far Left.

40%: Right > Far Right > Left > Far Left

36%: Left > Far Left > Right > Far Right

19%: Far Left > Left > Right > Far Right

The pairwise comparisons would look like this (I have put the pairwise victories here in bold, and left the defeats in plain text):

Far Right vs. Right = 5% vs. 95%

Far Right vs. Left = 45% vs. 55%

Far Right vs. Far Left = 45% vs. 55%

Right vs. Left = 45% vs. 55%

Right vs. Far Left = 45% vs. 55%

Left vs. Far Left = 81% vs. 19%

Left (who was also the IRV winner) has won all of his pairwise contests, and is therefore a Condorcet winner.

The same information can also be expressed as a matrix. The row marked “Far Right” represents Far Right’s score in her pairwise comparison with each other candidate. A candidate whose row consists only of victories, such as “Left” in this example, is a Condorcet winner.

Far Right Right Left Far Left

Far Right 5% 45% 45%

Right 95% 45% 45%

Left 55% 55% 81%

Far Left 55% 55% 19%

In this example, and surely many others, IRV and Condorcet’s method produce the same results. However, they do not always do so. Lets take example 3, An election between a “Right” candidate, a “Center” candidate, and a “Left” candidate.

33%: Left > Center > Right

16%: Center > Left > Right

16%: Center > Right > Left

35%: Right > Center > Left

Here is a diagram, which might make it easier to conceptualize:

Left Center Right

33% 32% 35%

<--------16% 16%---------->

33%----------> <-----------35%

The IRV tally would go like this:

Left Center Right

33% 32% 35%

round one: Center is eliminated, transferring 16% to each remaining candidate.

+16% ~~32%~~ +16%

49% 51%

Right wins the election using IRV. If, however, the losing candidate Left was deleted from the ballots, or withdrew from the race just before the election, Center would have beat Right with a crushing 65-35 majority. (Likewise, without Right in the race, Center would have soundly beat Left by 67-33.)

Indeed, those who voted Left > Center > Right will regret their votes given the above result, and wish that they had voted Center > Left > Right instead, which would have resulted in the election of their second choice (Center) rather than their last choice (Right).

If voters anticipate this sort of result before the election, then they have a strong incentive not to raise the position of a compromise candidate on the ballot, so that they can ensure that he or she is not eliminated early on. (This is an application of the compromising strategy.) While such strategy might produce an optimal result given good information prior to the election, the strategically altered vote no longer communicates the true preferences of the voters, and there is a danger that voters will make an unnecessary compromise which costs their sincere favorite the election.

Plus, if voters fail to anticipate such a result, then they will be left with a widely-regretted and unstable outcome like the one above.

If IRV voters are going to use the compromising strategy, it seems that it would be much better for them to raise the compromise candidate into an equal position with more preferred candidates, rather than a superior position, so that their preferences are less severely distorted. This is a good argument to allow equal ranking in IRV.

Condorcet produces a different result given this example. Here are the pairwise comparisons:

Left vs. Center = 33% vs. 67%

Left vs. Right = 49% vs. 51%

Center vs. Right = 65% vs. 35%

Or, as a matrix:

Left Center Right

Left 33% 49%

Center 67% 65%

Right 51% 35%

Center wins all of her pairwise comparisons (and quite easily, at that), and is therefore a Condorcet winner. IRV fails to elect Center because she is eliminated before any votes can be transferred to her, leaving a choice between the two wing candidates. Condorcet does not make the same mistake, since it doesn’t eliminate any candidates before it looks at the later preferences on the ballots.

In the examples used so far, a clear Condorcet winner has been present, and so there is no difference between results given by different Condorcet methods. Now let’s look at some of the different methods for choosing a winner when a cycle is present and no Condorcet winner exists.

I am presenting these methods as a sort of progression from the most simple Condorcet method, which is minimax, through Smith + minimax and Schwartz sequential dropping, to the more subtle Condorcet methods: beatpath and ranked pairs.

It is very rare that these more complex methods would produce a result different from minimax or Smith + minimax, and there are situations where a change from one of these to beatpath or ranked pairs would not be worth the added complexity. However, when a (single-winner) collective decision is very important and the resources to make the calculation are available, I would recommend the beatpath or ranked pairs methods.

I.A.3.a. minimax / successive reversal / Simpson[*]

Let’s take an example where no Condorcet winner exists, example 3.1. This is an imaginary election between Bush, Gore, and Nader, where Bush has lost a little bit of ground since 2000, and Nader has gained a lot of ground from Gore. This example involves truncated ballots, on which Bush voters refuse to rank either Gore or Nader, and some Gore voters rank neither Nader nor Bush.

Note that a ballot marked Nader > Gore is completely equivalent to a ballot marked Nader > Gore > Bush; the position of Bush in last place is implied, since he is the only other candidate. Hence such a ballot is not truncated in any meaningful way. A ballot which only indicates Bush as the first choice is equivalent to a ballot which indicates Bush > Gore = Nader.

45%: Bush

12%: Gore

14%: Gore > Nader

29%: Nader > Gore

Or, in diagram form:

Nader Gore Bush

29% 26% 45%

29%------------->

<-------------14%

The pairwise comparisons:

Nader vs. Gore = 29% vs. 26%

Nader vs. Bush = 43% vs. 45%

Gore vs. Bush = 55% vs. 45%

The same information expressed as a matrix:

Nader Gore Bush

Nader 29 43

Gore 26 55

Bush 45 45

In this example there is a cycle, which leaves no candidate unbeaten. The simplest way to resolve this cycle is to drop or disrecognize the weakest defeat, and to go on doing this until an unbeaten candidate emerges. This method is sometimes known as “successive reversal,” and because the resulting winner is the candidate whose worst loss is the least bad, “minimax.”

Actually, I can't recommend minimax for use in elections, because it fails the mutual majority criterion, the Condorcet loser criterion, and the Smith criterion. The Smith criterion corresponds to the Smith set, which is defined in the next section.

Criteria summary for minimax

Criteria passed: majority, Pareto, Condorcet, monotonicity

Criteria failed: mutual majority, Smith, participation, consistency, independence of clones, Condorcet loser, later preferences

Strategic vulnerability: Some compromising incentive and some burying vulnerability. The amount of each depends largely on defeat strength definition, but in general minimax should have worse burying problems than Smith-efficient methods with the same defeat strength definition, because of its mutual majority criterion failure.

I.A.3.aa. Winning votes versus margins

I wrote above that minimax drops the weakest defeat until an unbeaten candidate emerges. But how do we decide which defeat is the weakest? The two most common defeat strength definitions are margins and winning votes (WV).

The solution to example 3.1 above depends on which of these you choose. The margins of the three pairwise comparisons are 3% (29%-26%), 2% (45%-43%), and 10% (55%-45%). The smallest margin is 2%, which is the margin of Bush’s defeat of Nader. Using margin-based minimax, this defeat would be dropped, leaving Nader unbeaten and declaring him the winner.

The winning vote totals for the defeats are 29%, 45%, and 55%. The weakest defeat in a WV method is Nader’s defeat of Gore, with a magnitude of 29%. So, using WV-based minimax, this defeat is disrecognized, and Gore is declared the winner.

I prefer Condorcet methods that are based on winning votes rather than margins, because I believe that margins methods do not allow for stable counterstrategies, potentially causing very serious strategic turmoil. (Also, it seems odd to me that Nader should win in the example above, since he never achieves more than 43% of the vote in any of his comparisons, whereas Bush has 45% of the vote in all of his.) I write more about the strategic vulnerability of margins here.

If all of the voters rank all of the candidates, then margin-based results will be identical to magnitude-based results, because a defeat that has a greater magnitude will also have a correspondingly greater margin. There will be no difference between magnitude and margin results in any of the other examples below.

(Notice that IRV gives the victory in this case to Bush, an outcome that seems unfair, and problematic in terms of third party participation. (That is, Nader’s presence in the race once again has a sort of “spoiler effect,” in that Gore would have won the election instead of Bush if Nader had been deleted from the ballots.))

I.A.3.b. Minimal dominant set (Smith set) // minimax

A fairly simple variation on the basic minimax method of breaking cycles is to first exclude candidates who are not a member of the top cycle in the first place. One way of doing this is to only include members of the minimal dominant set, also known as the Smith[*] set, or the GeTChA set (which stands for Generalized Top Choice Axiom)[*].

The minimal dominant set is the smallest possible set of candidates such that every candidate inside the set beats every candidate outside of the set.

Here is an example where eliminating non-members of the Smith set will make a difference, example 4. The preference rankings and the resulting pairwise comparison matrix:

6 voters: A>B>C>D

6 voters: D>C>A>B

6 voters: B>C>A>D

5 voters: D>A>B>C

4 voters: C>A>B>D

4 voters: D>B>C>A

2 voters: B>C>D>A

2 voters: A>C>B>D

1 voter: A>C>D>B

A B C D

A 24 14 19

B 12 23 20

C 22 13 21

D 17 16 15

When conceptualizing Condorcet cycles, I often find it helpful to draw diagrams like the one below. If an arrow is drawn from A-->B, it means that A beats B in pairwise comparison. The number assigned to the arrow is the magnitude of the defeat. When possible, I put the numbers on the outer edge of the line to avoid crowding. Otherwise, I try to put them close to the point of the arrow, such as the B-->C defeat with 23 magnitude below. Later on, a double-sided arrow will symbolize a pairwise tie.

Using these sorts of diagrams, it is more readily apparent that A B and C all beat D, and that they form a cycle with each other.

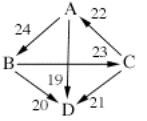
In this case, the Smith set consists of A, B, and C, but not D, because A, B, and C each beat D in pairwise comparisons.

Plain minimax will in fact choose D as the winner, like so: first his defeat by A is dropped, that being the weakest defeat. There is still no unbeaten candidate, so his defeat by B is dropped, and then finally his defeat by C, leaving D unbeaten and therefore the winner of the election.

D is what is known as a Condorcet loser, that is a candidate who loses all of their pairwise contests. It seems undesirable for a Condorcet loser to win an election, and excluding non-members of the Smith set prevents this.

With a Smith set + minimax combination, D is eliminated first in this example. There is still no unbeaten candidate, so A’s defeat by C, which is the weakest, is dropped, leaving A as the winner.

Criteria summary for Smith//minimax

Criteria passed: Smith, majority, mutual majority, Pareto, Condorcet, Condorcet loser, monotonicity

Criteria failed: participation, consistency, independence of clones, later preferences

Strategic vulnerability: Some compromising incentive and some burying vulnerability. The amount of each depends largely on defeat strength definition, but in general Smith-efficient methods should have better strategic resistance than their Smith-failing counterparts.

I.A.3.bb. Sequential dropping

There is a subtle but important difference between the sequential dropping rule and the minimax rule. The minimax rule is to drop the weakest defeat until there is an unbeaten candidate.

The sequential dropping rule is to drop the weakest defeat that's in a cycle until there is an unbeaten candidate.

Sequential dropping naturally passes the Smith criterion without having to add a special provision as in Smith/minimax. Sequential dropping may be the reasonably good base method that is easiest to define and explain.

Criteria summary for sequential dropping

Criteria passed: Smith, majority, mutual majority, Pareto, Condorcet, Condorcet loser

Criteria failed: participation, consistency, independence of clones, later preferences, monotonicity

I.A.3.c. Union of minimal undominated sets (Schwartz set)

The union of minimal undominated sets is the same as the minimal dominant set, as long as there are no pairwise ties (the odds of which should be statistically negligible in a public election, but may come in to play when a smaller group is voting). The union of minimal undominated sets is also known as the Schwartz set[*], or the GOCHA set (Generalized Optimal CHoice Axiom)[*].

An undominated set is a set of candidates not beaten by any candidates outside the set. A minimal undominated set does not contain other undominated sets. It is possible for more than one minimal undominated set to exist at once, so the complete Schwartz set is the union of all of them.

The Schwartz sets is always a subset of the Smith set, that is it may be the entire Smith set, or only one or a few members of the Smith set, but it will not include candidates outside the Smith set. Hence if any of the two sets is smaller, it will be the Schwartz set.

Here is an example where they are different, example 5. I will omit the preference rankings this time. The double-sided arrow in the diagram indicates a tie (the magnitude of which is not important).

A B C D

A 54 56 50

B 46 58 52

C 44 42 60

D 50 48 40

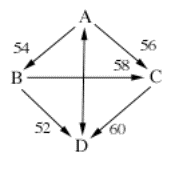
Here, the minimal dominant set is all the candidates, because there is no smaller set of candidates who beats all of the other candidates.

There is however a single minimal undominated set, which consists only of A. Hence A is the only member of the Schwartz set.

Like the Smith set, the Schwartz set usually contains more than one candidate if no Condorcet winner exists. So, it is not a satisfactory method in itself for finding a single winner, but it is useful as a tool and a criterion for other methods.

I.A.3.d. Schwartz sequential dropping

If a Condorcet winner does not exist, Schwartz sequential dropping first excludes non-members of the Schwartz set. Next it drops the weakest defeat, that is, it replaces the weakest defeat with a pairwise tie. If there is still no unbeaten candidate, it recalculates the Schwartz set and excludes non-members, and then drops the weakest remaining defeat within the set. This process continues until there is an unbeaten candidate, who is then declared the winner.

Here is an example where this is different from Smith + minimax, example 6:

A B C D E

A 108 106 102 90

B 92 88 120 114

C 94 112 84 118

D 98 80 116 104

E 110 86 82 96

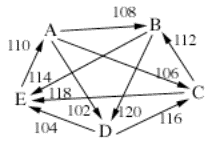
In this case the Smith set is all five candidates. minimax will then go on dropping the weakest defeats until an unbeaten candidate emerges. In this case, the minimax winner is A, whose worst loss is least bad. (A’s worst loss is 110-90, while the other candidates’ worst losses are 112-88, 116-84, 120-80, and 118-82.)

The Schwartz set is also all five candidates, and Schwartz sequential dropping also begins the same way, by dropping the weakest defeats one by one. However, look what happens when we get to this point:

A B C D E

A -- -- -- 90

B -- 88 120 114

C -- 112 84 118

D -- 80 116 --

E 110 86 82 --

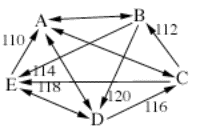
The Smith set would still be all five candidates, because there is no smaller set that beats all candidates outside that set. However, the Schwartz set at this point is reduced to only B, C, and D. B, C, and D constitute a minimal undominated set in that none of them are beaten by A or E, and there is no smaller set of undominated candidates within B, C, and D. Both A and E have at least one defeat by the B C D set, so they cannot qualify as an undominated set. The whole set of candidates A, B, C, D, and E does not qualify as a minimal undominated set because it contains the smaller undominated set B, C, and D.

So, A and E are eliminated at this point because they are no longer part of the Schwartz set. The matrix of the remaining candidates would look like this:

B C D

B 88 120

C 112 84

D 80 116

The 112-88 defeat would be dropped next, leaving B as an undefeated candidate, and the winner using Schwartz sequential dropping.

I.A.3.e. Beatpath / cloneproof Schwartz sequential dropping

The rule for this method, invented by Markus Schulze[*], can be explained in two very different ways. That is, there is a procedure to apply it based on ‘beatpaths,’ and there is another procedure very similar to the Schwartz sequential dropping procedure above, but with one subtle difference. Both approaches will be explained, but although they seem different on the surface, they always produce the same results as each other, and therefore can essentially be considered the same method.

Let’s look at the ‘cloneproof Schwartz sequential dropping’ (CSSD) procedure first, since we have just come from the other SSD. The CSSD procedure is identical to the SSD procedure, except for its stopping point. SSD stops when one or more candidates is unbeaten (if more than one, then it is a tie). CSSD, on the other hand, doesn’t stop dropping defeats until there are no longer any cycles in the remaining Schwartz set.

I will give an example to clarify, example 7. There are 12 voters and 3 candidates: A, R, S, and T.

3 voters: A>R>S>T

2 voters: A>T>R>S

1 voter: A>S>T>R

3 voters: S>T>R>A

2 voters: R>S>T>A

1 voter: T>R>S>A

A R S T

A 6 6 6

R 6 8 5

S 6 4 9

T 6 7 3

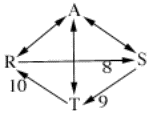
Given these ballots, regular SSD declares A to be the winner right away without dropping any defeats, because he is the only candidate who has no defeats against him.

However, the current Schwartz set still includes all four candidates. That is, A does indeed constitute in himself a minimal undominated set, but R, S, and T together also form a minimal undominated set, as A doesn’t beat any of them, but only ties them. Furthermore, the defeats from R to S, S to T, and T to R constitute a cycle.

Therefore, Cloneproof SSD is not satisfied yet, because there is still a cycle in the Schwartz set. CSSD proceeds by dropping the weakest defeat, which is T’s 7-5 defeat over R. Now the new Schwartz set consists only of A and R, as both are minimal undominated sets in themselves. There is no cycle is the new Schwartz set, so the procedure is finished, and a tie is declared between A and R.

Now, you may be wondering what is so cloneproof about this method. You might even be wondering what ‘cloneproof’ means.

First of all, a set of clones is defined as a group of candidates who always appear lumped together on the ballots of every voter. In example 7 above, R, S, and T constitute a set of clones. That is, every voter either prefers A to all member of the R S T set, or every member of the R S T set to A. This suggests that R, S, and T have a lot more similarity between them than any have in common with A. Hence the term ‘clones.’

What ‘clone’ doesn’t mean (that it might be imagined to mean) is that a set of candidates are always ranked equal to each other. It only means that there are no other candidates ranked in between them.

A method is ‘cloneproof,’ if it meets ‘independent of clones’ criterion defined by Nicolaus Tideman.[*] A method is independent of clones if the addition or subtraction of clones doesn’t change the winning status of either a clone set or a non-clone candidate. That is, it shouldn’t be to the advantage or disadvantage of any candidate to have a lot of similar candidates running. This is an important property because these sorts of advantages and disadvantages might artificially lower or raise the size of the field of candidates, as well as causing unfair results.

In terms of degree, all of the Condorcet versions above are very highly resistant to clones, that is the addition of clones will only make a difference in some very specific circumstances involving pairwise ties, such as the example above. CSSD only differs in that it has perfect resistance to clones, rather than only almost-perfect resistance to clones. For public elections, the difference between SSD and CSSD is negligible, because the probability of pairwise ties between competitive candidates is extremely low. The difference between the two methods only stands a chance of being important when smaller numbers of people vote, such as in a committee or legislature.

Now that I have explained the ‘cloneproof Schwartz sequential dropping’ procedure, I will also explain the elegant ‘beatpath’ procedure which produces the same results. To illustrate what a beatpath is, I will bring back example 4, just because it is a fairly straightforward one to work with.

A B C D

A 24 14 19

B 12 23 20

C 22 13 21

D 17 16 15

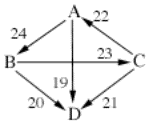
B does not have a pairwise win over A, but there is a beatpath from B to A, and there is also a beatpath from A to B. The question is, which beatpath is stronger?

A beatpath is basically a series of defeats that links one candidate to another. If A beats B and B beats C, then there is a beatpath from A to C.

Each beatpath has a certain strength. The strength of a beatpath is equal to the weakest defeat that makes up the beatpath. (Again, this can be measured in magnitudes or margins. In this example it makes no difference, but I will use magnitudes as I demonstrate it here.) Let’s take the beatpaths from A to B and B to A.

beatpath A-->B = A --24--> B = 24

beatpath B-->A = B --23--> C --22--> A = 22

The total strength of the A-->B beatpath is 24, while the strength of the B-->A is only 22. Since A’s beatpath to B is stronger than B’s beatpath to A, A has a beatpath win over B. The winner of the election is the candidate or candidates who have no beatpath wins against them.

Let’s look at the rest of the beatpaths contests:

beatpath A-->C = A --24--> B --23--> C = 23

beatpath C-->A = C --22--> A = 22

beatpath A-->D = A --24--> B --23--> C --21--> D = 21

beatpath D-->A : none exists

Note that D doesn’t have a beatpath to A here. Actually, D doesn’t have a beatpath to anyone, since she loses all of her pairwise comparisons. This is of course an automatic win for A if he has any beatpath whatsoever to D.

Also note that there are multiple beatpaths from A to D, such as the simple beatpath straight from A to D (with a magnitude of 19), the A-->B-->D beatpath (which has a magnitude of 20), and the A-->B-->C-->D beatpath, which has a magnitude of 21, and which is therefore the one that is used. The rule in the beatpath procedure is to always use the strongest available beatpath. (Of course in this case it doesn’t matter, since D loses no matter what, but this is an important rule to remember.) To finish up:

beatpath B-->C = B --23--> C = 23

beatpath C-->B = C --22--> A --24--> B = 22

beatpath B-->D = B --23-->C --21--> D = 21

beatpath D-->B : none exists

beatpath C-->D = C --21--> D = 21

beatpath D-->C : none exists

So, the winning beatpaths are A-->B, A-->C, A-->D, B-->C, B-->D, and C-->D. It is clear that the beatpath winner is A, who is the only candidate who does not have a beatpath win against him, and who in fact wins his beatpath contests with all of the other candidates.

Interestingly, beatpath victories are transitive. That is, if any candidate R has a beatpath win against another candidate S, and S has a beatpath win against T, then R necessarily has a beatpath win against T. Likewise, if X has a beatpath tie with Y, and Y has a beatpath tie against Z, then X will also have a beatpath tie against Z. If L has a beatpath tie against M, and M has a beatpath win against N, then L will have a beatpath win against N. And so on.

So, beatpath always produces a coherent and complete ordering of the candidates. In example 4 above, this order is A>B>C>D. Another example of a coherent ordering would be F>G=H>I. (G and H are equal to each other, but both preferred over I.) An incoherent ordering would be something involving a cycle, such as F>G>H>I>F. This kind of cyclical result can of course happen in pairwise comparisons, which is why cycle-breaking methods are needed, but such cycles cannot emerge from beatpath comparisons.

Criteria summary for beatpath

Criteria passed: majority, mutual majority, Smith, Pareto, Condorcet, monotonicity, independence of clones, Condorcet loser

Criteria failed: participation, consistency, later preferences

I.A.3.f. Ranked pairs

Along with beatpath, the other Condorcet method that is widely considered to be superior is called ranked pairs, or Tideman’s method[*]. It shares many of beatpath’s desirable properties, including the fact that it never picks a Condorcet loser, always picks a member of the Smith set, is monotonic, and is entirely independent of clones.

In example 3.1, both beatpath and ranked pairs choose Gore, like minimax did. In example 4, both beatpath and ranked pairs choose A, like Smith + minimax did. In example 6, both beatpath and ranked pairs choose B, as Schwartz sequential dropping did. In example 7, both beatpath and ranked pairs call a tie between A and R.

Ranked pairs works on a similar basis as these methods, but sort of in reverse. The methods above start with all of the pairwise comparisons, and then drop the defeats one by one if necessary, with the weakest first.

Ranked pairs, on the other hand, starts with a blank slate, and then adds the defeats one by one, with the strongest first. As the defeats are added, they are locked in place, and cannot be subsequently disrecognized. However, if a defeat is about to be added which would contradict any of the stronger, previously locked defeats, it is skipped, that is, it is disrecognized and not added in the first place. This goes on until all the defeats have been considered, and the winner is the candidate or candidates who have no standing (non-skipped) defeats against them. Once again I will illustrate this with example 4.

A B C D

A 24 14 19

B 12 23 20

C 22 13 21

D 17 16 15

We will consider the defeats in order from strongest to weakest, deciding with each one whether to lock it in or skip it. Note that the first two strongest defeats will always be kept, as it is impossible to form a cycle with only one or two defeats; three is the minimum needed.

24: A-->B keep

23: B-->C keep

[22: C-->A] skip

A’s defeat by C must be skipped, because it would cause a cycle: A-->B-->C-->A.

21: C-->D keep

20: B-->D keep

19: A-->D keep

So, the kept defeats are A-->B, B-->C, C-->D, B-->D, and A-->D. The winner is the unbeaten candidate, A. Like beatpath, ranked pairs also produces full orderings of the different candidates, which is helpful in situations where the next choice in the ordering can be acted on if the first choice is found to be impossible. In this case the order is once again A>B>C>D.

Although beatpath and ranked pairs should produce the same result the vast majority of the time, their results are not identical. There are not known to be any heavy criteria in favor of one method over the other, so the choice between them may be something of a matter of taste. Below are two examples where beatpath and ranked pairs produce different results.

Example 8:

7: B>A>C>D

5: C>D>A>B

5: D>B>A>C

4: C>A>D>B

4: B>C>A>D

2: D>A>B>C

2: A>D>B>C

1: A>C>D>B

A B C D

A 14 17 18

B 16 20 11

C 13 10 21

D 12 19 9

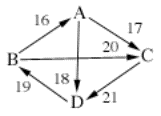
Below are the beatpath comparisons. (Winning beatpaths are in bold, losing beatpaths are in plain text.)

beatpath A-->B: A --18--> D --19--> B = 18

beatpath B-->A: B --16--> A = 16

beatpath A-->C: A --18--> D --19--> B --20--> C = 18

beatpath C-->A: C --21--> D --19--> B --16--> A = 16

beatpath A-->D: A --18--> D = 18

beatpath D-->A: D --19--> B --16--> A = 16

beatpath B-->C: B --20--> C = 20

beatpath C-->B: C --21--> D --19--> B = 19

beatpath B-->D: B --20--> C --21--> D = 20

beatpath D-->B: D --19--> B = 19

beatpath C-->D: C --21--> D = 21

beatpath D-->C: D --19--> B --20--> C = 19

So, again the winning beatpaths are A-->B, A-->C, A-->D, B-->C, B-->D, and C-->D. Therefore beatpath declares A the winner, with a total ordering of A>B>C>D.

Here is the ranked pairs procedure:

21: C-->D keep

20: B-->C keep

[19: D-->B] skip

18: A-->D keep

17: A-->C keep

16: B-->A keep

In this example, B’s worst loss is 19 and A’s worst loss is only 16. This is basically the reason why A wins using beatpath. The reason that B’s magnitude 19 loss doesn’t count against him in ranked pairs is that it is the weakest loss within the B C D cycle, therefore it is skipped, and B goes onto win. Note that in this example B, the ranked pairs winner, wins her pairwise comparison with A, the beatpath winner. In the next example however, the opposite is true. Example 9:

8: B>D>E>A>C

8: C>A>B>E>D

8: E>B>A>D>C

5: E>A>C>B>D

5: D>C>B>E>A

4: D>A>C>B>E

4: D>C>A>B>E

3: A>B>C>D>E

3: E>A>D>C>B

2: C>E>B>D>A

2: A>B>D>C>E

1: D>E>C>A>B

1: B>A>D>C>E

1: A>D>C>B>E

1: E>C>B>A>D

A B C D E

A 31 35 32 23

B 25 22 38 36

C 21 34 19 30

D 24 18 37 29

E 33 20 26 27

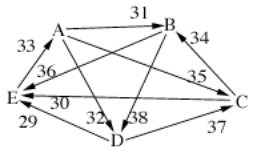
Beatpath contests:

beatpath A-->B: A --35--> C --34--> B = 34

beatpath B-->A: B --36--> E --33--> A = 33

beatpath A-->C: A --35--> C = 35

beatpath C-->A: C --34--> B --36--> E --33--> A = 33

beatpath A-->D: A --35--> C --34--> B --38--> D = 34

beatpath D-->A: D --37--> C --34--> B --36--> E --33--> A = 33

beatpath A-->E: A --35--> C --34--> B --36--> E = 34

beatpath E-->A: E --33--> A = 33

beatpath B-->C: B --38--> D --37--> C = 37

beatpath C-->B: C --34--> B = 34

beatpath B-->D: B --38--> D = 38

beatpath D-->B: D --37--> C --34--> B = 34

beatpath B-->E: B --36--> E = 36

beatpath E-->B: E --33--> A --35--> C --34--> B = 33

beatpath C-->D: C --34--> B --38--> D = 34

beatpath D-->C: D --37--> C = 37

beatpath C-->E: C --34--> B --36--> E = 34

beatpath E-->C: E --33--> A --35--> C = 33

beatpath D-->E: D --37--> C --34--> B --36--> E = 34

beatpath E-->D: E --33--> A --35--> C --34--> B --38--> D = 33

So, the beatpath winner is A, with a complete ordering of A>B>D>C>E.

Ranked pairs procedure:

38: B-->D keep

37: D-->C keep

36: B-->E keep

35: A-->C keep

[34: C-->B] skip

33: E-->A keep

32: A-->D keep

[31: A-->B] skip

[30: C-->E] skip

[29: D-->E] skip

In this example, B’s worst loss (34) is again worse than A’s (33), and again B’s worst loss is forgiven because it is the weakest loss in its cycle, the B C D cycle. While in the last example it is B who knocks out A, this time it is E who knocks him out. A’s 31-25 defeat of B comes too late in the order to be kept, since it would form a cycle between B, E, and A.

The ranked pairs winner is B, with a complete ordering of B>E>A>D>C.

Criteria summary for ranked pairs

Criteria passed: majority, mutual majority, Smith, Pareto, Condorcet, monotonicity, independence of clones, Condorcet loser

Criteria failed: participation, consistency, later preferences

I.A.3.ff. The river method

The river method is a variation on ranked pairs first proposed by Jobst Heitzig. The major difference between river and ranked pairs is that river does not lock more than one defeat against the same candidate. The river method is generally thought to share the major positive qualities of beatpath and ranked pairs.

I.B.3.g. Other Condorcet methods

I have presented the series of Condorcet methods above as a sort of progressive sequence leading up to beatpath and ranked pairs, where understanding of those at the beginning of the sequence facilitate understanding of those at the end. This sequence of Condorcet methods actually have a lot in common, in that they tend to favor the candidate whose worst loss is least bad, although some of them build further refinements on this basic principle.

This principle seems to be the most attractive approach to breaking cycles, for various reasons, but it is not the only approach that has been considered. I will briefly describe some of the other Condorcet methods that have been proposed.

I.B.3.g.i. Raynaud

In the Raynaud method, the candidate with the strongest pairwise defeat among remaining candidates is eliminated, until only one remains.[*] When a candidate is eliminated, the pairwise comparisons between that candidate and other candidates are also removed from consideration at the same time, and hence a strong defeat by that candidate will not matter to any candidate left in the race after she has been eliminated.

I.B.3.g.ii. Dodgson

The method invented by C.L. Dodgson (better known as Lewis Carroll) sums each candidate's margins of defeat and chooses the candidate with the smallest sum.[*] (If a candidate is a Condorcet winner, then of course they would not have any margins of defeat, and would therefore win with a sum of 0.)

I.B.3.g.iii. Kemeny

While some Condorcet methods put most of their focus on determining a single winner, or the option listed highest in the final ordering of options, Kemeny is more geared towards creating a complete ordering of options, and hence might be useful in situations where that is especially important.

Kemeny evaluates each ordering of the options in terms of the sum of preference reversals on each ballot that would have to be performed in order to produce that transitive ordering. The complete ordering which requires the fewest preference reversals is the final result of the method.[*]

For example, let's say that the ordering we are evaluating is A>B>C>D, and there are 5 ballots where the ordering is A>D>B>C. To change an A>D>B>C ballot to A>B>C>D would require two preference reversals, that is a reversal of the preference between B and D, and the preference between C and D. The other preferences, such as the preference between A and D, are consistent between the A>D>B>C ordering and the A>B>C>D ordering.

As one would have to make 2 adjustments on each of these 5 ballots, then one would have to make 10 adjustments in total. You could therefore express the Kemeny score for the A>B>C>D ordering given those ballots as -10. Kemeny would combine this score with the scores from the other ballots in the election. If the A>B>C>D ordering ended up having the least negative sum, than it would be selected.

Of course, if these 5 ballots were the only ones cast in the election, then the final result of the Kemeny tally would be the ordering A>D>B>C, since it is not necessary to reverse any of the preferences on any of the ballots to produce that ordering, and so the sum of negative scores is 0.

Although his writings on the subject of breaking cycles are somewhat unclear to contemporary readers, it is now believed by many that the method proposed by Kemeny in the 20th century is the same as the one intended by Condorcet.

I.B.3.g.iv. Condorcet completed by IRV

Using this method, if no Condorcet winner exists, the outcome is determined by instant runoff voting.

I.B.3.h. A strategy problem

Are beatpath and ranked pairs flawless? No. They meet a great deal of desirable criteria, but some problems may remain. Perhaps the most perplexing issue with Condorcet methods is a strategic one. However, this is not the sort of 'compromising'[*] or 'favorite betrayal' strategy which we have seen so far, where voters play it safe and downrank their sincere first choice in favor of a compromise candidate. Condorcet methods minimize this strategy to the degree that it is possible to do so.

The strategy that Condorcet is most vulnerable to is sometimes known as 'burying'[*] or 'offensive order reversal.' An example of it would be putting your sincere second favorite in last place in order to increase the chances that your favorite will win.

I have addressed this issue in greater depth, in my proposals for the cardinal pairwise method and the iterative pairwise procedure.

I.B.3.i. Cardinal-weighted pairwise comparison^[*]

Cardinal pairwise or CWP for short.

Cardinal pairwise uses cardinal ballots (e.g. rating from 0-100) to provide an alternative definition of defeat strength. If candidate A pairwise beats candidate B, the strength of the defeat would be defined as follows: For each A>B voter, and only for A>B voters, subtract B’s rating from A’s rating, to get the rating differential. Sum the A>B rating differentials to get the A>B defeat strength.

I consider cardinal pairwise to be a superior defeat strength definition for resolving sincere majority rule cycles and for preventing the strategic creation of insincere cycles. For more details, please see my cardinal pairwise paper.

Criteria summary for cardinal pairwise

Criteria passed: majority, mutual majority, Smith, Pareto, Condorcet, monotonicity, Condorcet loser

Criteria failed: participation, consistency, later preferences, independence of clones (unless the criterion is adapted such that clones receive the same rating from all voters)

Strategic vulnerability: In my opinion, minimal compromising incentives and manageable burying incentives.

I.C. Miscellaneous single winner methods

Compared to the total number of single winner systems that have been proposed, and even compared to the number of systems which have some interesting merit or use, the amount of systems that I have described so far is miniscule. I have chosen to focus on certain methods because they seem to represent a progression towards certain desirable properties. However, I will finish the section on single-winner methods by briefly describing a few more systems which are interesting in different ways.

I.C.1. Candidate withdrawal option IRV

The rules for candidate withdrawal option IRV (CWO-IRV) are the same as for regular IRV, but at the end of the initial tally, candidates have the option of withdrawing and ordering a new tally with them removed from consideration.[*] If the initial tally failed to elect the Condorcet winner, than a candidate withdrawal would be likely correct the mistake. In example 3, Right won the initial IRV tally. However, if Left decided to use the candidate withdrawal option, the 33% of the vote initially assigned to her would be transferred to Center at the beginning of the tally, and Center would win easily.

In this example it is very reasonable for Left to withdraw, since she has no chance of winning herself, and since she would obviously be doing her voters a service by allowing them to elect their second choice rather than their last choice. CWO-IRV invites a process of bargaining between candidates in these situations, which is a feature of the method that may either be considered attractive or unattractive.

More complicated examples exist where the withdrawal of different candidates could affect the outcome in different ways. For example, two candidates can be in a situation where if one withdraws, the other wins, and vice versa. In such cases bargaining could be expected to be more intense.

CWO-IRV may be difficult for the public to accept. However, if the public does accept it, it could be a very good voting method. It tends toward Smith-efficiency, while possibly dampening some of the strategic issues associated with Condorcet methods.

I.C.2. Candidate withdrawal option in general

Of course, CWO can be used with other methods aside from IRV. It might be attractive in an STV tally for similar reasons to its attractiveness in IRV. It might be helpful in pairwise methods as well, in that it might allow the candidates to "catch" the result of strategic incursions before the result is permanent, and that it may tend to resolve sincere cycles by dropping defeats between similar candidates (as cardinal pairwise does). However, it is possible that behind-the-scenes bargaining over withdrawals could produce unfair results in some cases.

I.C.3. Lowest two elimination runoff

This method is a sort of hybrid between IRV and Condorcet. The rule is that if no candidate has a majority of votes assigned to them, a pairwise comparison is held between the two candidates with the lowest totals of assigned votes, and the loser is eliminated. This continues until a candidate accumulates a majority, or until only one candidate remains.[*]

This method is actually Condorcet efficient in that it will always elect a Condorcet winner if one exists, and never elect a Condorcet loser if one exists. It may serve as an interesting bridge between IRV and Condorcet, but it seems to have some potential problems at the same time. In example 4, it holds a comparison between Nader and Gore, eliminates Gore, and then Nader loses in the subsequent runoff against Bush. This result is not entirely unreasonable, but it may be problematic in that it gives Bush voters a strategic incentive to truncate their ballots. Basically, it doesn’t offer any technical advantages to the other Condorcet methods, but it might be easier to explain, and doesn’t have any severe drawbacks.

I.C.4. Coombs

Where IRV eliminates the candidate with the fewest first choice votes, Coombs eliminates the candidate with the most last choice votes.[*] Otherwise, the two methods are the same.

I.C.5. Bucklin

Bucklin is a ranked ballot system. If any candidate has a majority of first choice votes alone, then that candidate is elected. Otherwise, if any candidate has a majority of first and second choice votes, that candidate is elected. Otherwise, if any candidate has a majority of first and second and third choice votes, they are elected. And so on. If two candidates achieve a majority at the same stage of the count, then the candidate with the larger total at that stage is elected.[*]

I.C.6. Ratings summation (also known as "range voting" or "cardinal ratings")

Voters are asked to assign a point value within a specified range to each candidate. For example, they might be asked to rank each candidate on a scale of 0 to 100, using only whole numbers. The candidate with the highest total of points is the winner.[*]

It is expected that voters in many cases will give each candidate in the election either the highest or the lowest possible rating (such as 100 and 0 given the scale above), in order to maximize the power of their ballot. If this is the case, then cardinal ratings becomes similar in effect to approval voting.

Criteria summary for ratings summation

Criteria passed: monotonicity, participation, consistency, later preferences, Pareto

Criteria failed: majority, mutual majority, Condorcet, Condorcet loser, Smith, independence of clones

Strategic vulnerability: Strong compromising-compression and burying-compression incentives. It is commonly believed that, in a contentious electorate, most voters will tend to give most candidates extreme ratings (highest possible or lowest possible). If all voters give only extreme ratings, the method is equivalent to approval voting.

I.C.7. Equal-ranking-allowed IRV versions

Although IRV typically does not allow equal rankings, it should. There are two basically different ways to count equal rankings in IRV; I call these ER-IRV(fractional) and ER-IRV(whole).

I.C.7.a. ER-IRV(fractional)

1. Ranked ballots, with equal rankings allowed.
2. Do a ballot count for each candidate as follows: Add 1 to the vote total of a candidate for each ballot which ranks them alone in first place. Add 1/n to the vote total of a candidate for each ballot on which they are in an n-candidate tie for first place. (By first place, I mean the highest ranking given to a non-eliminated candidate.)
3. Eliminate the candidate with the lowest vote total.
4. Repeat steps 2 and 3 until only one candidate remains.

I.C.7.b. ER-IRV(whole)

(Note that the only difference between this an ER-IRV(fractional) is in step 2.

1. Ranked ballots, with equal rankings allowed.
2. Do a ballot count for each candidate as follows: Add 1 to the vote total of a candidate for each ballot which ranks them alone in first place. Add 1 to the vote total of a candidate for each ballot on which they are tied for first place. (By first place, I mean the highest ranking given to a non-eliminated candidate.)
3. Eliminate the candidate with the lowest vote total.
4. Repeat steps 2 and 3 until only one candidate remains.

Here is example 9.1, in which ER-IRV(fractional) and ER-IRV(whole) produce different results.

41: A>B>C

10: B>A>C

4: B>C>A

30: C=B>A

15: C>B>A

ER-IRV(fractional) tally:

A B C

41 14+15=29 15+15=30

+10 eliminate +19

51 49

ER-IRV(whole) tally:

A B C

41 14+30=44 15+30=45

eliminate +41

85 45

II. Multiple winner voting methods

Again, a multiple winner method selects multiple winners from a single field of candidates, where a single electorate is voting.

The typical example of this is a multi-seat legislature, such as a senate or city council, which is elected in multi-member districts, rather than each seat on the legislature being voted on by a separate electorate. For example, instead of each seat on a city council being voted on separately by members of different neighborhood districts, the entire city would vote together to determine the entire composition of the council.

Multiple-winner methods provide the opportunity for proportional representation (PR). While in a single-winner election it is possible to completely ignore the will of a given minority, the goal of proportional representation is to provide representation for all segments of the electorate such that the representation of a group in the set of elected options is in proportion to the relative size of the group within the electorate.

For example, if there is a set of voters who constitute 30% of the electorate, there is no guarantee that they will have any input in determining the outcome of a single winner election. However, in a proportional election filling 100 seats in a council, they should in theory be able to determine how 30 of those seats are filled.

In example 10, let’s say that there is a city with a 100 seat council. There are three major political parties: the Republicans, the Democrats, and the Greens. If it was to be decided via a series of single winner elections, it would be broken up into 100 equally-sized districts, with each district deciding one seat. For the sake of simplicity, let’s imagine that each one of these ten districts votes for the four different parties according to the same ratio, that is:

15%: Green > Democrat > Centrist > Republican

30%: Democrat > Centrist > Green > Republican

10%: Centrist > Democrat > Republican > Green

10%: Centrist > Republican > Democrat > Green

35%: Republican > Centrist > Democrat > Green

A plurality system might award all 100 seats to the Republican party (if everyone voted for their first choice). In this case 65% of the voters would basically be unrepresented.

Two round runoff and IRV would probably award all 100 seats to the Democratic party (if people voted for their first choice in the first round of the two round system, and if people cast non-strategic ballots in IRV). Condorcet would probably award all 100 seats to the Centrist party. Neither of these results seem particularly fair or inclusive.

Now, let’s imagine that instead of dividing the city into 100 separate districts, you were to have a single city-wide election based on proportional representation. Without going into the specifics, a generic PR method would be expected to award 15 of the 100 seats to members of the Green party, 30 to the Democrats, 10 to the Centrists, and 35 to the Republicans.

PR systems do not always fill an entire legislature with a single electorate and a single field of candidates, but may instead build a legislature out of a series of multiple winner chunks. An election can be considered to be PR as long as it uses multiple member districts, and allocates the seats within those districts proportionally. Given the same city above, it is possible to break up the 100 seats into 100 separate single-member districts (which would be the non-proportional method above), and it is possible to have 1 single 100-member district (which is the first proportional method above). However, it is also possible to break the city into 10 multiple member districts, which each decide how 10 of the seats are filled. Or it could be 5 multi-member districts which each decide 20 seats. Or 7 multi-member districts of different sizes which decide different numbers of seats. And so on.

Given the same example 10, if there were 5 districts of 20 seats each (each with the same distribution of preferences as above), than each district would probably award 3 seats to the Greens, 6 seats to the Democrats, 4 seats to the Centrists, and 7 seats to the Republicans. When multiplied by 5 to find the overall composition of the council, these numbers are the same as the single 100-member district method. However, of course this will not always be the case, since distribution of political preferences will probably vary from area to area, and because the numbers won’t usually be so tidy.

In general, higher district magnitudes lead to higher proportionality, since they allow for more precise representation of smaller groups. However, there are sometimes political reasons why people will want to maintain smaller district boundaries, for example, in order to assure more local representation.

Even if a council is formed according to proportional representation, it will usually still make decisions based on majority rule. However, the fact that PR was used is very important nonetheless.

For one thing, there may be some intrinsic value in having fuller discourse that takes into account a wider range of perspectives, even if there are some groups that rarely on the winning side of a vote.

Also, there is the problem that in single winner-based legislatures, the majority of a majority may be an overall minority. For example, let’s say that IRV elects a legislature full of Democrats. Let’s say that there is an issue which a majority of Democrats (both elected Democrats and voting Democrats) is in favor of, but an overall majority is opposed to. The issue would most likely pass given a single-winner IRV-based council, but fail if PR was used. The same criticism can be made of any other single winner system. In a PR system, majorities are more likely to shift in the legislature depending on the issue under discussion. In an ideal PR system, whether or not an issue has majority support in the legislature should correspond very closely to whether it would have majority support if the general public could vote on it.

II.A. Non-proportional multi-winner methods

Although multiple winner elections provide the opportunity for proportional representation, this opportunity is not always taken advantage of.

II.A.1. At large plurality / block voting

One of the most common multiple winner systems is known as ‘at large plurality,’ or ‘block voting.’ Using this system, voters have as many votes as there are seats to be decided. Let’s call this number S. Each voter can vote once each for any S candidates (but cannot vote more than once for any single candidate). The S candidates with the most votes are selected to fill the S seats.

In example 11, there are 10 seats to be decided, there are 10,000 voters, and there are 20 candidates, 10 Democrats and 10 Republicans. (We’ll call them D1 through D10 and R1 through R10.) The party preferences are as follows:

5,100 voters: Democrat

4,900 voters: Republican

Assuming that party preference is the primary factor in voters’ decisions, the results will look a lot like this:

D1: 5,100 votes. D2: 5,100 votes. D3: 5,100 votes. D4: 5,100 votes. D5: 5,100 votes. D6: 5,100 votes. D7: 5,100 votes. D8: 5,100 votes. D9: 5,100 votes. D10: 5,100 votes.

R1: 4,900 votes. R2: 4,900 votes. R3: 4,900 votes. R4: 4,900 votes. R5: 4,900 votes. R6: 4,900 votes. R7: 4,900 votes. R8: 4,900 votes. R9: 4,900 votes. R10: 4,900 votes.

The 10 Democratic candidates will be elected, and none of the Republican candidates will be elected. Obviously this is not a proportional result. (Most proportional systems would award 5 seats to each party.)

II.A.2. Other non-proportional methods

It is possible to design similar non-proportional methods based on various single winner methods, such as two-round runoff, Borda, IRV, or Condorcet. These are subject to the most of the same criticisms. That is, that they do not provide adequate diversity of representation, and they can set up a situation where a majority of a majority (or not even a true majority) is able to hold complete sway despite the fact that they are an overall minority.

II.B. Semi-proportional methods

These methods are called semi-proportional because they may under certain circumstances produce proportional result, but there is no actual guarantee that there will be proportionality of any kind. The more likely outcome is a kind of partial proportionality.

II.B.1. Cumulative voting

The rules for cumulative voting are very similar to the rules for at-large plurality, but with one important difference: voters are allowed to allocate more than one vote to a single candidate. This makes it so that voters who constitute a minority have the ability to increase their chances of electing candidates, by dividing their votes between fewer candidates. Let’s apply this to example 11.

5,100 voters: Democrat

4,900 voters: Republican

Now, the question is how many candidates each party should run. If the Democrats were to run 10 candidates again, and each Democratic voter voted for all 10 of them, each candidate would again receive 5,100 votes. However, let’s say that the Republicans only ran 9 candidates. Also, let’s assume that they were able to organize their supporters effectively so that each candidate received a roughly equal number of votes. (In real life this is sometimes done by rotating the ballots so that different candidates are on top of the party lineup, and asking supporters to vote for the top-listed candidate.) Each of the 9 Republican candidates would receive roughly 5,444 votes. These 9 would have the highest vote totals, meaning that they would get elected, leaving only one seat for the Democrats. Obviously it is a big risk for the Democrats to run 10 candidates!

Below is a table showing how many votes each Democratic or Republican candidate would receive given a certain number of candidates running from that party (assuming the constant number of voters 5,100 and 4,900, respectively).

Democrats Republicans

# of candidates votes per candidate # of candidates votes per candidate

10 5100 10 4900

9 5667 9 5444

8 6375 8 6125

7 7286 7 7000

6 8500 6 8167

5 10200 5 9800

4 12750 4 12250

One can see that the best strategy for one party depends on what strategy the other party uses. If the Democrats were to shoot for 7 seats, then the Republicans would be best off running 6 candidates, thus winning 6 of the 10 seats. However, if the Democrats and the Republicans both aimed for 6 seats, then the Democrats would win 6, leaving the Republicans 4.

It turns out that, given these vote totals, the two parties reach a strategic equilibrium when the Democrats run 6 candidates, the Republicans run 5 candidates, and each party wins 5 seats.

Of course, this assumes that both parties have a fairly accurate projection of their total number of supporters. The less clear this is, then the more difficult it will be to organize an effective strategy, and the less likelihood of proportionality there will be.

So, it takes a serious amount of organizing by the parties to get their best result. Also, if voters have significant preferences between the candidates of their favorite party, then things become more difficult.

In addition, there is no mechanism that allows a voter to support a favored long-shot candidate as their first choice and then have their full voting strength count for a compromise candidate if the first choice proves unwinnable. Hence, candidates are at a serious disadvantage if they are initially perceived to be unlikely to win; the perception will reinforce itself and create itself as reality.

II.B.2. Limited voting and the single non-transferable vote

Limited voting is almost identical to cumulative voting, but with one difference: voters are given fewer votes than there are seats to be filled. For example, in an election to fill 10 seats on a council, each voter might be given only 7 votes. They may still choose to give them all to a single candidate or divide them up among several candidates.

If voters are only given one vote in a multi-seat election, then this is known as the ‘single non-transferable vote” (SNTV). SNTV is a kind of limited voting.

Limited voting is similar to cumulative voting from the point of view of strategy and proportionality. Both strongly favor groups that are able to organize an effective collective voting strategy prior to the election.

II.C. Proportional methods

II.C.1. Party list

By far the most common method of proportional representation on the level of national legislatures is the party list method. Using this method, each party is represented on the ballot by a list of candidates. Usually there are as many candidates on each party's list as there are seats to be filled in the election. The lists will be in ranked order from first to last.

Each voter votes for one party. The number of seats awarded to each party is determined by the number of votes that they receive, processed by some proportional allocation formula. The party will then fill those seats with the candidates from the top of their list. For example, if a party is awarded 6 seats in a legislature, then the first 6 candidates on their list will fill those seats.

II.C.1.a. Open lists and closed lists

Countries differ in whether they use ‘open’ or ‘closed’ party lists. In a closed list system, the order of each party’s list is fixed at the time of the election, having been determined by the party leadership. Of course, the list is public at that time, and so voters know whom they are voting for when they choose a party. However, they do not have an opportunity to change the order of the list.

In an open list system, there is a list of candidates from each party on the ballot. However, in addition to choosing a party, voters for that party are able to indicate preferences for candidates within their chosen party, hence helping to determine the order of the list, and therefore which candidates actually gain seats if the party wins them. The most common open list method is that voters are able to vote once for their candidate of choice, and the list is then ordered from candidates who received the most votes to candidates who received the fewest votes.

While the open list system is proportional by party, and does allow voters some opportunity to control the composition of their chosen party, there are still some problems. For one thing, it reinforces the power of political parties in government, and makes it especially difficult for independent candidates to gain office.

Also, like many other systems, if a voter’s first choice is a small party which does not seem likely to have enough votes to gain a seat, then the voter is likely to abandon their favorite and vote instead for a more winnable party.

Also, in determining the order of the lists, there may be similar second-guessing. Voters may again hesitate to vote for an underdog who doesn’t seem to stand much of a chance of getting a seat, and vote instead for a candidate who seems closer to the margin of the number of votes needed. On the other hand, voters might also hesitate to vote for a favorite candidate from their party who seems to be so well-supported that she seems to be assured of getting a seat. However, if all of the voters from the party think that way and vote for someone else, then a highly popular candidate will end up not getting elected through sheer error and disorganization. These problems are addressed by the single transferable vote method, which I will get to after further discussion of party list formulas.

II.C.1.b. Allocation formulas

If there are ten seats up for grabs in an election, and one party gets 40% of the vote, then it seems pretty clear that that party deserves 4 of the 10 seats. However, things are not always quite this simple. Take example 12: There are 5 seats, 100,000 voters, and two parties in contention, party A and party B. 68,000 people vote for A and 32,000 vote for B. How many of the 5 seats should each party get?

II.C.1.b.i. Largest remainder

One way to allocate seats is through the largest remainder method. The first step in this method is to establish a quota, such that each party is guaranteed one seat for every quota that they receive. Once all whole quotas have been accounted for, if there are still unfilled seats, then those seats go to the parties who have the largest remainder of votes after those quotas have been subtracted.

II.C.1.b.i.aa. Hare quota

The most immediately intuitive quota is the Hare quota. It is simply the number of votes cast divided by the number of seats, or (V ÷ S).[*] If there are 100,000 voters and 100 seats, then the quota would be 100,000 ÷ 100 = 1,000 votes. Let’s apply the Hare quota to example 12.

100,000 votes. 5 seats. Hare quota = 100,000 ÷ 5 = 20,000 votes.

party A: 68,000 ---(+1 seat)---> 48,000 ---(+1 seat)---> 28,000 ---(+1 seat)---> 8,000

party B: 32,000 ---(+1 seat)---> 12,000

At this point, 4 seats have been allocated, and one remains. No party has any more whole quotas, so the seat is given to the party with the largest remainder. In this case, it is party B, who has a remainder of 12,000, while party A only has a remainder of 8,000. B is awarded one more seat, and the final result is 3 seats for A, and 2 seats for B.

II.C.1.b.i.bb. Droop quota

While the Hare quota may seem self-evident, consider for a moment an election where there were 100,000 voters, and only one seat available. What should the quota be in this case? If you used the Hare quota, you would get 100,000 ÷ 1 = 100,000 votes. In this case, the quota would be quite meaningless, since it requires unanimity. Of course, one would skip straight to the largest remainder part of the procedure, and the result would be the same. But it is this problem which first alerted people to the fact that the Hare quota isn’t quite perfect.

What seems more intuitive is that in a single winner election the appropriate quota should be a majority, that is 50,001 votes. This is the notion that led to the Droop quota, which is (votes ÷ (seats + 1)) +1, or (V ÷ (S + 1)) + 1.[*]

In general, given S seats and V votes, the Droop quota makes sense because it is the smallest number of votes that a candidate can hold while still being assured that there are not S other candidates who hold a greater or equal total of votes. To see why this is the case, let's imagine for a moment that the quota is equal to (V÷(S+1))+1. If S+1 candidates each had a quota of votes, then their combined total would be ((V÷(S+1))+1) x (S+1), which is equal to V + S + 1. Thus, the combined total of votes must be greater than the votes cast, which is impossible.

Given 100,000 votes and 5 seats, the Droop quota would be (100,000 ÷ (5 + 1)) + 1 = 16,667.67. Let’s apply this to example 12 as well.

A: 68,000 -(+1s)--> 51,332.33 -(+1s)--> 34,664.67 -(+1s)--> 17,997 -(+1s)--> 1,329.33

B: 32,000 -(+1s)--> 15,332.33

In contrast to the Hare quota, 4 whole Droop quotas can be awarded to party A. Since all the seats have been allocated based on whole quotas, there is no need to look at the highest remainders. Thus, the final result is 4 seats for A, and only 1 seat for B.

To confirm that this is a more fair result, consider what would happen if party A was to split itself into two separate parties with equal support.

A1: 34,000

A2: 34,000

B: 32,000

Using the Hare quota, A1 and A2 would each gain a seat and have a remainder of 14,000. B would also gain a seat, and have a remainder of 12,000. There would be two seats left to allocate, and these would go to the two parties with the highest remainders: A1 and A2, producing a total result of 4 for A and 1 for B, the same result that the Droop quota produced anyway. Using the Droop quota, the extra division would make no difference.

So, the problem with the Hare quota is that in theory it can encourage the wholly artificial division of a party for strategic gain only. Put another way, it can arbitrarily punish voters for investing a full quota in a party where less than a quota will do, and where investing the extra votes can make a difference somewhere else.

II.C.1.b.i.cc. Newland-Britton quota

While the formula for the Droop quota is (V ÷ (S + 1)) + 1, the Newland-Britton quota (NB quota) is merely (V ÷ (S + 1)).[*]

The extra vote in the Droop quota is intuitive in that it automatically prevents more than the desired number of seats from being allocated in the case of a tie. Take example 12.1, an election with 3 seats to be filled, 400 voters, and two parties, each with 200 votes.

The Newland-Britton quota would be (400 ÷ (3 + 1)) = 100. Unless there is another mechanism is in place to prevent it, each party will gain two seats, and the number of desired winners will be exceeded.

The Droop quota, on the other hand would be (400 ÷ (3 + 1) + 1 = 101. One seat would be granted to each party, and then a tie would be declared between them for the largest remainder and hence the third seat.

This is the basic rationale behind the Droop quota, but there is a small problem with it as well, which I will illustrate using example 12.2. There are 9 seats and 100 voters. There are in reality two parties, the Republicans and the Democrats, but while the Republicans are together on one list (R), the Democrats have divided themselves into 5 separate lists (D1 through D5), and very effectively split their voting support among the lists.

The Droop quota is (100 ÷ (9 + 1)) + 1 = 11.

R: 51 ---(+4 seats / -44 votes)---> 7

D1: 10

D2: 10

D3: 10

D4: 10

D5: 9

Since the Republicans have 51 votes to the Democrats' 49, and there is an odd number of seats, the Republicans should be expected to win the majority of the 9 seats. However, using the Droop quota as above, the Republicans win only 4 seats based on whole quotas, leaving a remainder of 7. Since all 5 Democratic party lists have larger remainders than 7, they scoop up all of the remaining 5 seats.

The Newland-Britton quota, however, is (100 ÷ (9 + 1)) = 10.

R: 51 ---(+5 seats / -50 votes)---> 1

D1: 10 ---(+1 seat / -10 votes)---> 0

D2: 10 ---(+1 seat / -10 votes)---> 0

D3: 10 ---(+1 seat / -10 votes)---> 0

D4: 10 ---(+1 seat / -10 votes)---> 0

D5: 9

Using the NB quota, the Republican list has enough votes for 5 whole quotas, and so the fifth Democratic list, which lacks a full quota, achieves no seats.

This is obviously the more fair result given the situation, and the Newland-Britton quota does seem tidier than the Droop quota, but what can be done about the over-allocation problem in example 12.1?

The solution applied by Irwin Mann to single transferable vote elections is that a candidate should not be awarded a seat unless they have more than a quota's worth of votes remaining, but when they actually are awarded a seat, only a quota's worth should be subtracted. The Newland-Britton quota, given this stipulation, is probably the most sensible and fair quota available. (Although I should note that the odds of it producing a different result in a public election, with large numbers of voters, are negligible.)

II.C.1.ii. Greatest average

An alternative to the largest remainder method is the greatest average method. Actually this is more commonly used for party list PR, while quotas are used primarily by the single transferable vote method.

The basic idea of greatest average is that a party’s eligibility for an additional seat, versus another party’s eligibility for that same seat, should depend on the average number of votes per seat that each party would have given that additional seat. Seats are allocated one by one, each time to the party with the greatest average votes per seat, until there are no more seats remaining to be allocated.

II.C.1.ii.aa. D’Hondt divisors

The most intuitive set of divisors are the D’Hondt divisors, which are simply the natural numbers 1, 2, 3, 4, and so on.[*] I will apply them to example 12:

1 2 3 4

A: 68,000 -1-(1s)--> 34,000 -2-(2s)--> 22,666.67 -4-(3s)--> 17,000

B: 32,000 -3-(1s)--> 16,000

The numbers under each divisor are simply the total votes for that party divided by the divisor. The size of the number under the first divisor determines a party's eligibility for their first seat, the number under the second divisor determines their eligibility for their second seat, and so on.

Here I have shown the first 4 allocations, and have not yet done the last one. I have numbered the allocations in the order that they are performed. The notation -4-(3)-->, in A’s row, means that the fourth seat allocated is given to A, raising his total of seats to 3.

You can see that the first seat was given to A, whose average for one seat is 68,000, higher than B’s average of 32,000. The second seat is also given to A, whose average for two seats, 34,000, is still higher than B’s average for one seat. However, the next seat is given to B, since A’s average for a third seat is 22,666.67, compared to B’s 32,000 average for its first seat. The next seat, however, goes to B, finishing up the diagram as shown above.

One seat remains to be allocated, and that seat goes to A. A’s average for 4 seats is 17,000 votes per seat, whereas B’s average for 2 seats is only 16,000. In fact, you could skip the earlier steps if you knew that it was going to come down to A getting a fourth seat versus B getting a second seat. Hence the final result is 4 seats for A, and 1 seat for B.

In this example, D’Hondt greatest averages produces the same results as Droop largest remainder, and in fact they almost always do so.

II.C.1.b.bb. Saint-Lagüe divisors

An alternate set of divisors exists, known as the Saint-Lagüe divisors. These are the odd numbers 1, 3, 5, 7, and so on.[*] Applying these to example 12:

1 3 5 7

A: 68,000 -1-(1s)--> 22,666.67 -3-(2s)--> 13,600 -4-(3s)--> 9,714.29

B: 32,000 -2-(1s)--> 10,333.67

Again I have left the fifth seat open, but in this case it goes to B, whose modified ‘average’ of votes for 2 seats is 10,333.67, while A’s modified average for 4 seats is only 9,714.29. So the final result is 3 seats for A, and 2 seats for B.

As Droop and D’Hondt usually produce the same results, as in this case, so do Hare and Saint-Lagüe. Hence, Saint-Lagüe can be criticized on the same basis as Hare.

II.C.1.c. Thresholds

Another factor in proportional representation is the existence or non-existence of minimum thresholds. Some countries that use party list PR impose a threshold, that is a certain percentage of the vote such that a party cannot gain a seat unless they receive at least that percentage, even if they would have been eligible for one or more seats under the general allocation rule. Thresholds are generally along the order of magnitude of 2.5% or 5%, although higher thresholds are possible.

The purpose of these thresholds is to reduce the number of parties in a legislature, and to keep out smaller parties. Therefore, for anyone who thinks that the participation of small parties can be beneficial, thresholds are very unattractive.

II.C.2. Single transferable vote

The party list proportional methods above all assume that political parties are the principle unit of democracy, and proportionality by party choice sufficiently covers the range of diversity within an electorate. Also, they provide strategic incentives for voters to avoid voting for candidates that seem to unlikely to win, or in a few cases, for candidates who seem too likely to win.

The single transferable vote (STV) principle, however, makes no assumptions about party unity, and in fact works just as well if political parties don’t exist. Also, it does an ingenious job of addressing these problems of redundant and wasted votes. In short, the single transferable vote principle seems to be the key to effective proportional representation.

To understand STV, it is perhaps best to being with an understanding of IRV, since IRV is in fact the single-winner version of STV, and was derived from STV. If you then add to this an understanding of quotas for seat allocation, you are most of the way there.

STV begins by establishing a quota. Usually the Droop or Newland-Britton quota is used. STV uses ranked ballots. Each person has one vote.

The basic idea of STV is as follows: If any candidate has a quota’s worth of first choice votes, then they are immediately elected. If a candidate has more than a quota’s worth, then the excess votes, called the surplus, are transferred to the subsequent choices on each individual ballot. An elected candidate retains no more than a quota’s worth of votes, and the rest are passed onward.

If these transferred votes create surpluses for another candidate, then their surpluses are transferred too, and so on until there are no more surpluses.

If all candidates with a quota have been elected, all surpluses have been transferred, and there are still seats remaining, the candidate with the fewest top choice votes is eliminated (as in IRV), and the votes which they had held are now transferred to the next choice on each individual ballot.

If there are any candidates that now have reached the quota as a result of this, their surpluses are transferred.

The rule in STV is that no candidates are eliminated until all existing surpluses have been transferred.

If there are still empty seats after the surpluses are transferred, then once again the candidate with the fewest top choice votes is eliminated.

This process goes on until either enough candidates to fill all of the seats have gained a quota, or until the amount of uneliminated candidates is equal to the number of seats to be filled.

An example is in order here, example 13. There are 3 seats to be filled, and 400 voters. I will use the Newland-Britton quota, which is (V÷(S+1)) = (400 ÷ (3 + 1)) = 100 votes.

170 voters: A>B>C>D>E>F

20 voters: B>A>C>D>E>F

30 voters: C>B>A>D>E>F

120 voters: D>E>F>A>B>C

50 voters: E>D>F>A>B>C

10 voters: F>E>D>A>B>C

These are the preference rankings. (I have put in bold the rankings that actually matter to the election. That is, the voting power of each ballot in this example is absorbed by the first one or two candidates listed, and the position of the later candidates is irrelevant.)

Below is the step by step process of an STV count, divided into a series of states and actions. In each state, the number listed for each candidate is the number of ballots currently assigned to them at that time. Each action consists of either electing a candidate and transferring their surplus, or eliminating a candidate. The tally is over when all 3 seats have been filled.

Candidates State 1 Action 1 State 2 Action 2 State 3

A 170 elect, -70 100 / elected 100 / elected

B 20 +70 90 90

C 30 30 30

D 120 120 elect, -20 100 / elected

E 50 50 +20 70

F 10 10 10

Candidates Action 3 State 4 Action 4 State 5 Action 6

A 100 / elected 100 / elected

B 90 +30 120 elect

C 30 eliminate, -30 eliminated

D 100 / elected 100 / elected

E +10 80 80

F eliminate, -10 eliminated eliminated

Candidates Elected?

A Yes

B Yes

C No

D Yes

E No

F No

The first action involves electing candidate A and transferring her surplus. (It is common for STV rules to transfer the largest surplus first when there is more than one.) Since all of the voters who chose A first chose B second, it is clear that all of the extra 70 votes will go to B. In action 2, D is elected and his surplus is transferred to E. Now there are no surpluses to transfer, there is still an unfilled seats, and there are 4 candidates who would like to have it. At this stage it is necessary to eliminate the candidate with the lowest total of votes, namely candidate F, who has only 10 votes. This brings candidate E’s total up to 80, but this is still not enough for a quota, so another candidate needs to be eliminated, this time candidate C, who has 30 votes. Now candidate C has enough for a quota and is elected. All three seats are filled, the tally is over, and the final result is that A, B, and D are elected.

By the way, sometimes there can be a situation where some ballots do not list all of the candidates, and where the ballots would still be in play but none of the candidates listed on the ballot are in play anymore (either because they have been eliminated or elected). Such ballots are then called exhausted ballots. If ballots become exhausted at some stage of the tally, then it is customary to actually lower the quota of votes needed for a seat, so that it is based on the number of non-exhausted ballots rather than the total number of ballots. I will not demonstrate this, however, and exhausted ballots won't be a factor in any of my examples.

II.C.2.a. Surplus transfer rules

In the basic definition of STV above, I wrote that “the excess votes, called the surplus, are transferred to the subsequent choice on each individual ballot.” However, there is a serious question here, that is: which votes are considered the excess votes, and hence which votes are transferred? Since different ballots are likely to list different candidates as their next choice, the decision of which ballots to transfer can affect the outcome of the election.

Early versions of STV chose the ballots to be transferred at random. More recent versions transfer all of the ballots, but at a common fractional value. This an intuitive solution, but it contains certain problems addressed by such refinements as the Meek transfer rule. I will describe all three of these in more detail now.

II.C.2.a.i. Random transfers

The simplest transfer rule for STV has an element of chance. When a candidate reaches a quota and generates a surplus, it is decided randomly which ballots will remain with that candidate and which will be transferred to subsequent choices. For example, if there is a quota of 100 votes, and a candidate receives 120 votes, then a randomly selected 20 of those votes are transferred in whole to subsequent candidates, while the remaining 100 have no further impact on the election.

Although this doesn’t give an inherent advantage to any particular candidates over another (as long as the ballots are properly shuffled), it is unsettling that a method can give different results depending on chance. Hence, when the resources to do so are readily available, it is probably always better to use a method of STV based on fractional transfers.

I will use example 14 to illustrate the difference between random and fractional transfer-based STV. There are again 400 ballots cast and 3 seats to be filled. Hence the Newland-Britton quota is again 100 votes.

90: A>C>D>B>E

90: A>D>C>B>E

120: B>D>A>C>E

40: C>D>A>B>E

50: D>C>A>B>E

10: E>C>D>A>B

(Again, only the rankings in bold are relevant to the election. If all of the voters truncated after the bolded entries, it would make no difference.) The critical juncture of this example is action 1, where A’s surplus is transferred. A will retain 100 votes, and pass along 80, but the question is where those 80 votes will go next. 90 of A’s 180 voters indicated C as their next choice, and the other 90 indicated D. Using random STV, there is no guarantee that the transferred ballots will have the same even proportion of later preferences. For example, below I have imagined that, simply by chance, 55 of the 80 ballots transferred list C as the next choice, and only 25 list D as the next choice.

Candidate State 1 Action 1 State 2 Action 2 State 3

A 180 elect,-80 100 / elected 100 / elected

B 120 120 elect,-20 100 / elected

C 40 +55 95 95

D 50 +25 75 +20 95

E 10 10 10

Candidate Action 3 State 4 Action 4 Elected?

A 100 / elected Yes

B 100 / elected Yes

C +10 105 elect Yes

D 95 No

E eliminate,-10 eliminated No

The result of C’s good luck in A’s surplus transfer is that he is elected, along with A and B. You should be able to verify that the result would have been A B and D instead, if A’s transfer had been closer to a 40-40 split.

II.C.2.a.ii. Fractional transfers

The most straightforward answer to this problem is to use fractional surplus transfers. Instead of reducing only some of the ballots at a whole value, fractional transfer STV transfers the same portion of all the ballots which went into creating the quota and surplus.

When a candidate reaches a quota and has a surplus, two complementary fractions are formed: the retention fraction and the transfer fraction. These two fractions add up to 1, so they can easily be derived from each other.

The retention fraction for the elected candidate is the fraction of each ballot that they need to retain in order to retain a full quota. Hence the formula for the retention fraction is the value of a quota divided by the total votes for that candidate, or Q ÷ total.

The transfer fraction is the remaining fraction of each ballot which is free to be transferred to subsequent choices. Thus it is 1 minus the retention fraction, or 1 - (Q ÷ total).

The transfer fraction can also be derived directly by dividing the surplus by the total amount of votes. That is, the total amount of votes minus the value needed for a quota, divided by the total amount of votes, or (total - Q) ÷ total. These two expressions are algebraically equivalent.

Note that if a candidate has exactly one quota’s worth of votes, then the retention fraction is Q ÷ Q = 1, and the transfer fraction is (Q - Q) ÷ Q = 0. This makes good sense, as the candidate will have to retain all of her votes in order to still have a quota, and will have nothing left over to transfer.

Below, I have applied the fractional transfer method to example 14. At the beginning, candidate A has 180 votes. The quota is 100 votes. Therefore, A's retention fraction after being elected is Q ÷ total = 100 ÷ 180 = .55...

The transfer fraction is (total - Q) ÷ total = (180 - 100) ÷ 180 = .44... This is the value at which each vote is transferred at. You can see that .55... and .44... added together equal 1. Therefore the whole strength of the vote is accounted for. I have abbreviated retention fraction and transfer fraction as rf and tf.

Candidate State 1 Action 1

A 180 elect, rf=100÷180=.55..., tf=(180-100)÷180=.44...

B 120

C 40 +(90 x .44...) = +40

D 50 +(90 x .44...) = +40

E 10

Candidate State 2

A 180x.55=100 / elected

B 120

C 80

D 90
E 10

Candidate Action 2

B elect, rf=100÷120=.833..., tf=(120-100)÷120=.166...

D +(120 x .166...) = +20

Candidate State 3 Action 3 Elected?

A 100 / elected Yes

B 120x.83=100 / elected Yes

C 80 No

D 110 elect Yes

E 10 No

The use of fractional transfers only differs from random STV in how it performs action 1. Both bring A’s total down to 100, of course. However, while random STV randomly picks 80 ballots from A’s 180, fractional transfer gives all 180 ballots a transfer fraction of .44..., resulting in the equivalent of 40 votes being transferred to both C and D (which is completely fair). In action 2, B is elected and transfers the equivalent of 20 votes to candidate D, bringing him up to a quota, so that the third seat is filled and the tally is over, with a final result of A, B, and D.

Although does not really come into play in this example, it is quite possible that a fractionally-valued ballot will subsequently become part of another surplus and hence be transferred yet again at a further reduced value. This can go on as long as candidates keep forming surpluses.

II.C.2.a.iii. Meek

Although the basic fractional transfer rule is quite good, there remains a sort of quirk in the procedure that can allow some people to have more voting power than others. Let’s say that there are two voters (among many in a public election), named Leroy and Chuck. Leroy’s sincere preference ranking is A>B>C, and Chuck’s sincere preference ranking is A>C>B. If both Leroy and Chuck vote sincerely, and A achieves a surplus, then their votes will be transferred at the same fractional value to B and C, respectively.

However, let’s say that Chuck gets crafty and votes instead for R>A>C>B, candidate R being an irrelevant candidate who is almost certain to be eliminated at some point. If candidate A achieves a surplus before R is eliminated, then Leroy’s vote will be reduced to a fractional value and transferred to B, while Ralph’s vote will remain with candidate R. (Remember that no candidates are eliminated until all existing surpluses have been transferred.) When candidate R does get eliminated, Chuck’s vote will be transferred to candidate C in whole, rather than in fractional part.

It is not at all uncommon that such a strategy will increase someone’s voting power in fractional transfer STV. And even if no one does this intentionally, the fact will remain that some people will end up having more voting power than others by virtue of having their vote tucked away somewhere else when one of their subsequent choices reaches a quota.

I will illustrate this problem using example 15. Here there are only 2 seats to be filled, which isn’t very good proportional representation at all, but makes for a simpler example. There are 300 voters. The Newland-Britton quota is 300 ÷ (2 + 1) = 100 votes.

130: A>B>C>R>S

60: B>A>C>R>S

60: C>A>B>R>S

30: R>A>C>B>S

20: S>A>C>B>R

First, I will apply the ordinary fractional transfer version of STV.

Candidate State 1 Action 1

A 130 elect, rf=100÷130=.77, tf=(130-100)÷130=.23

B 60 +(130 x .23) = +30

C 60

R 30

S 20

Candidate State 2 Action 2 State 3

A 130x.77=100 / elected 100 / elected

B 90 90

C 60 +20 80

R 30 30

S 20 eliminate, -20 eliminated

Candidate Action 3 State 4 Action 4 Elected?

A 100 / elected Yes

B 90 No

C +30 110 elect Yes

R eliminate,-30 eliminated No

S eliminated No

I think it is apparent that there is something kind of fishy about this result. Leaving the candidates R and S (who are designed to be irrelevant, and have no chance of winning a seat) out of the equation, the preference rankings would look like this:

130: A>B>C

50: A>C>B

60: B>A>C

60: C>A>B

B and C are even in terms of first choice votes, and out of the 180 voters who chose A over both of them, 130 prefer B, while only 50 prefer C. Why, then, did C win? Because the 130 A>B>C voters had their votes transferred to B at a steep fractional value (such that their power was reduced to the equivalent of 30 votes), while the 50 A>C>B votes were transferred at full value. By the time these 50 votes would have been transferred to A, A was already elected and had a fixed retention fraction, so they passed straight along to C.

Brian Meek proposed[*] to correct this problem by continually recalculating the retention fractions of each elected candidate when new votes are added to their total, so that a part of the new votes are absorbed and yet the candidate still retains exactly one quota. Since the change in one candidate’s retention fraction might alter the retention fraction needed by another candidate, the Meek method needs to holistically compute the set retention fractions that will result in each elected candidate having exactly a quota. In some cases, this may result in a series of algebraic equations with multiple variables. Although the application of Meek to this example is simple enough, in general Meek requires the use of a computer.

Candidate State 1 Action 1

A 130 elect, rf=100÷130=.77, tf=(130-100)÷130=.23

B 60 +(130 x .23) = +30

C 60

R 30

S 20

Candidate State 2

A 130x.77=100 / elected

B 90

C 60

R 30

S 20

Candidate Action 2

A +20, rf=100÷150=.66..., tf=(150-100)÷150=.33...

B recalculate. 60 +(130 x .33...) = 60 + 43.33... = 103.33...

C +(20 x .33) = +6.66...

S eliminate,-20

Candidate State 3 Action 3 Elected?

A 150x.67=100 / elected Yes

B 103.33... elect Yes

C 66.66... No

R 30 No

S eliminated No

Action 1 is the same in Meek as it was using plain fractional transfer. However, when S is eliminated in Meek, the extra 20 votes raises candidate A’s transfer fraction from .23 to .33. This in turn means that instead of only transferring the equivalent of 30 votes to candidate B, now the equivalent of 43.33 votes are transferred from A, giving B a total of 103.33, which is enough to get elected.

(By the way, if R had been eliminated as well, then A’s transfer fraction would have risen to .44..., B’s total would have risen to 117.77..., and C’s total would have risen to 82.22.... This second elimination is of course unnecessary, but I just mention it to point out that the contest between B and C is not particularly close using the Meek method.)

II.C.3. Comparison of a pair of outcomes by single transferable vote (CPO-STV)[*]

I should be clear from the beginning that although CPO-STV offers an extra degree of precision and fluidity, the general STV rule is very good. STV, based on Meek or fractional transfers, is an enormous improvement over virtually every other method of proportional representation. If for reasons of computational resources CPO-STV cannot be implemented, there is no need to feel ambivalent about switching to STV from at-large plurality, cumulative voting, party list voting, or the like. STV is a very effective system which gives true proportional representation without a reliance on political parties. With a high district magnitude, it substantially reduces the spoiler effect and lead to real diversity, responsiveness, and accountability within an elected body.

However, I have already mentioned that the single transferable vote method, when only used to elect a single seat, is equivalent to the IRV method. (Meek or fractional transfers are irrelevant in that case, since there is no meaning in transferring a surplus when there is only one candidate to be elected. Not even the choice of quota makes a difference, as long as it is at least a majority of the total vote.) Hence, the criticisms of IRV are also applicable to STV in multi-winner elections. Basically, the problem is with sequential eliminations. STV can eliminate a candidate who might have gone on to win given another elimination order, that is, if another non-winning candidate had been eliminated earlier instead of later.

In general this problem seems to be less severe the more seats there are to be filled by STV. That is, it shouldn’t really effect the overall proportionality of a multi-seat STV election. It seems that it would come into play on more of a small scale, for example in situations where a group of somewhat like-minded candidates were competing for a single seat.

It is not hard to take examples where IRV fails to produce a Condorcet winner in a single-seat election and build them into a multiple-seat election. This is the idea behind example 16. There are 3 seats to be filled, 400 voters, and 5 candidates: Ralph Nader, Al Gore, George Bush, Andre the Giant, and M.C. Escher. I will use the Newland-Britton quota, which is 400 ÷ (3 + 1) = 100. (This time I haven’t even added any irrelevant preference rankings, because I’m trying to keep things as simple as possible!)

160 voters: Escher > Bush > Gore

60 voters: Andre > Nader > Gore

90 voters: Andre > Gore > Nader

36 voters: Nader > Gore

12 voters: Gore > Nader

12 voters: Gore > Bush

30 voters: Bush > Gore

Just to make it clear what I’m after, let me show you the preference rankings without Escher or Andre (and without the votes that they have that are necessarily tied up in quotas).

56: Nader > Gore > Bush

42: Gore > Nader > Bush

12: Gore > Bush > Nader

90: Bush > Gore > Nader

This is a classic example of a case where IRV fails to select the Condorcet winner, who is Gore. The idea is that Nader is once again a sort of second-order spoiler using IRV, since although he is unable to win, his presence in the race changes the winner from Gore to Bush. (This situation is similar to example 3.1, except that Bush voters rank Gore next instead of truncating, and therefore Gore is a clear Condorcet winner among the three.)

First, I will do the ordinary STV tally. (In this example, the Meek method behaves the same as the ordinary fractional transfer method.)

Candidates State 1 Action 1 State 2

Escher 160 elect, rf=100÷160=.625, tf=.375 160x.625=100 / elected

Andre 150 150

Nader 36 36

Gore 24 24

Bush 30 +(160 x .375) = +60 90

Candidates Action 2 State 3 Action 3

Escher 100 / elected

Andre elect, rf=100÷150=.67, tf=.33 150x.67=100 / elected

Nader +(60x.33) = +20 56 +42

Gore +(90x.33) = +30 54 eliminate,-54

Bush 90 +12

Candidates State 4 Action 4 Elected?

Escher 100 / elected Yes

Andre 100 / elected Yes

Nader 98 No

Gore eliminated No

Bush 102 elect Yes

So, just as IRV elects Bush in the single-winner case above, STV also elects Bush along with Andre and Escher in this 3-winner equivalent. This is a problem for STV.

For example, given a situation where a small party has just enough votes for a single seat, the introduction of a new candidate within that party might tip the balance of the vote in the opposite direction within that party, or possibly split the vote so badly that no member of that party gets a seat at all. This might cause voters to vote strategically to avoid the elimination of a compromise candidate, and it might cause potential additional candidates to decide not to run, thus reducing the amount of competitive candidates and therefore the overall level of accountability of the elected officials.

This is the problem, but what is the solution? It is fairly clear that it should involve a method which somehow combines the virtues of Condorcet and STV, that is a Condorcet-STV hybrid. However, it turns out that devising such a method is extremely hard to do. There are methods based too firmly on Condorcet which fail to be fully proportional, and on the other hand there are methods that try to tack Condorcet onto STV, which tend to be somewhat clumsy and incomplete.

By far the most satisfactory proposal so far is CPO-STV, that is the comparison of pairs of outcome by single transferable vote, which was first proposed by Nicolaus Tideman.

How does it work? To begin with, recall that Condorcet’s method compares every candidate with every other candidate to find the winner. Since Condorcet is a single winner method, the outcome of a Condorcet election is simply the one winner. Hence Condorcet is comparing a series of outcomes with one another, but these outcomes are simple and the comparisons are easily scored.

The outcome of a multiple winner election, on the other hand, is not only a single candidate, but rather the full set of candidates who gain seats. In the example above, Escher + Andre + Bush constitutes one possible outcome. Escher + Andre + Gore is another. Actually, since there are 3 seats and 5 candidates, there are 10 possible outcomes for the election, which are as follows:

Escher + Andre + Nader

Escher + Andre + Gore

Escher + Andre + Bush

Escher + Nader + Gore

Escher + Gore + Bush

Andre + Nader + Gore

Andre + Nader + Bush

Andre + Gore + Bush

Nader + Gore + Bush

(Thankfully, the order of the candidates is irrelevant.) So, the aim of CPO-STV is to treat each of these outcomes as if they were a candidate in a Condorcet election, that is, to compare them with each other, put the results into a matrix, chose the Condorcet winner if it exists, and if not, to chose the winner based on some completion method. That makes sense so far, but the big question is how to score the outcomes against one another.

I will try to go step by step through the method Tideman proposed, using the example above. Let’s say that we want to compare the outcome Escher + Andre + Gore to the outcome Escher + Andre + Bush.

The first step is to eliminate all of the candidates who are not in either outcome, and transfer their votes. In this case, the only candidate not in either outcome is Nader. If his votes are transferred, then you have state 1 below. (By the way, I am still using fractional transfers here, but I am leaving out the computations and only writing down the overall effect.)

Candidate State 1 Action 1 State 2 Action 2 State 3

Escher 160 transfer,-60 100 100

Andre 150 150 transfer,-50 100

Gore 60 60 +50 110

Bush 30 +60 90 90

The next step is to transfer surpluses. In CPO-STV, the rule is that you only transfer surpluses of candidates who are in both outcomes. This is important because transferring a surplus from a candidate only in one outcome to a candidate only in the other outcome would make it so that the candidate's own surplus is counting against them.

Escher and Andre have surpluses, and are in both outcomes. Hence both surpluses are transferred. In state 3, Gore has a surplus, but it is not transferred because he is not in both outcomes.

Now it is possible to compare the two outcomes. This is done simply by summing the vote totals held by candidates in each outcome, that is the number of votes held in the final state. In this case it would end up like so:

Escher + Andre + Gore = 100 + 100 + 110 = 310

Escher + Andre + Bush = 100 + 100 + 90 = 290

Therefore, the pairwise comparison between Escher + Andre + Gore, and Escher + Andre + Bush results in a 310-290 victory of EAG over EAB. These are the numbers that you would put into the pairwise comparison matrix.

Now I will repeat the process and compare Escher + Andre + Gore to Escher + Andre + Nader. First, Bush is taken out of the mix and his votes transferred to Gore. Next, Escher transfers his surplus to Gore, and Andre’s surplus is divided up between Nader and Gore. Gore has the only surplus now, but it is not transferred, because he is not in both outcomes.

Candidate State 1 Action 1 State 2 Action 2 State 3

Escher 160 transfer,-60 100 100

Andre 150 150 transfer,-50 100

Nader 36 36 +20 56

Gore 54 +60 114 +30 144

Escher + Andre + Nader = 100 + 100 + 56 = 256

Escher + Andre + Gore = 100 + 100 + 144 = 344

Therefore, EAN vs. EAG = 256 vs. 344. At this point, it should be fairly clear that EAG will win all of its pairwise comparisons, since any outcome without both Escher and Andre in it would be rather strange (as they have so many votes), and it has been shown that of the three outcomes that do contain both of them, EAG is a clear Condorcet winner.

However, I will do one more comparison, in order to further demonstrate the surplus rule, and to help illustrate why an outcome that doesn’t include both Escher and Andre doesn’t have a chance.

Lets take Escher + Andre + Nader vs. Escher + Nader + Gore. Again, Bush is removed, resulting in the same initial state as the last comparison. Escher’s surplus is transferred to Gore, but Andre is not in both outcomes, so he keeps his surplus. Also, Gore holds onto his surplus once he achieves it.

Candidate State 1 Action 1 State 2

Escher 160 transfer,-60 100

Andre 150 150

Nader 36 36

Gore 54 +60 114

Escher + Andre + Nader = 100 + 150 + 36 = 286

Escher + Nader + Gore = 100 + 36 + 114 = 250

So, EAN soundly beats ENG, and again I believe that any outcome containing Escher and Andre will beat any outcome not containing Escher and Andre.

More to the point, I believe that there is no outcome which beats (or ties) Escher + Andre + Gore. Hence it is a clear Condorcet winner, and the final result of the CPO-STV election. Looking back at my analogy of the competition for the third seat to a single-winner race, I think it is clear that Gore deserves to win, since he is a clear Condorcet winner in that context.

Note that, given the choice to use CPO-STV for an election, a number of options remain. One can choose whichever surplus transferring rule one prefers. One can chose whichever quota one prefers. Also, one can choose whichever Condorcet completion mechanism one prefers, in the case of a cycle between outcomes. For example, one could chose to use minimax, beatpath, ranked pairs, etc.

The most obvious difficulty with CPO-STV is its computational cost. Certainly CPO-STV will almost always require the use of a computer, and if it is an election with a large enough number of voters and candidates, a particularly strong computer may be necessary, and perhaps a certain amount of time. There are probably a number of situations where the benefits of CPO-STV over elimination-based STV are not worth the extra resources that it requires.

However, it is cheering to note that the computational cost of CPO-STV is not quite as daunting as it may appear at first, because it is possible to use computational shortcuts that do not subtract from the integrity of the method. That is, one does not always have to compute every cell in the comparison matrix. There are often several outcomes which can be safely dismissed from consideration from the beginning, either because they contain candidates who can’t lose or candidates who can’t win.[*]

Also, instead of computing the whole matrix, one can start with a likely initial outcome (such as the outcome based on regular STV) and test it against the other non-dismissed outcomes. If it beats all of them, it is the final result. If there is another outcomes which beats or ties it, then you can check that outcome against the others, and so on until you have found the set of contending outcomes which beat all the other outcomes. This saves the considerable trouble of comparing all of those other outcomes to each other. One can then apply one’s preferred Condorcet completion method to the contender set.

There is a further cost-saving version of CPO-STV, called local CPO-STV (or CPO-STV lite)[*], which substantially reduces cost, but slightly compromises the CPO-STV method. This uses the same cost-saving measures as above, plus instead of comparing contender outcomes to all other outcomes, it only compares them to outcomes which only differ from them by the substitution of one candidate, and to other members of the contender set. This can lead to a different result from CPO-STV, but such differences should be extremely rare. Hence local CPO-STV occupies the territory between STV and CPO-STV in terms of both cost and accuracy.

II.D. Combined systems

Given a multiple winner situation, one is of course free to combine different election method that one finds attractive for different reasons. I will briefly mention the two most common examples of this on a national level: parallel voting and mixed member proportional representation.

II.D.1. Parallel

A parallel system generally a refers to a legislature where some seats are elected by a single-winner system in small districts, and some seats are elected by a form of proportional representation in multi-member districts, usually party list PR. Generally each voter will have a dual ballot that gives them a choice between candidates for their district, as well as a choice between party lists. The ratio between these two types of seats is variable. Sometimes it is half and half, but usually there are more of one than the other.

Take example 17. Here there are four parties, A, B, C, and D. There is a legislature with 100 seats. There are 50 seats which are won in single member districts, and 50 seats which are allocated according to party list proportional representation.

List Vote District Seats Won List Seats Won Total Seats

A 40% 26 20 46

B 30% 18 15 33

C 20% 4 10 14

D 10% 2 5 7

The result is simple enough. The 50 list seats are allocated in simple proportion to the party’s share of the list vote, and this total is added to their totals from the district elections. Note that in the district elections the larger parties are over-represented, and the smaller parties are underrepresented. (This is extremely common in single-winner elections.) This disproportionality carries through to the final result, although its degree is reduced by half.

II.D.2. Mixed member proportional representation

The mixed member proportional (MMP) system, also known as the additional member system, is similar to a parallel, but with one added dimension. Like a parallel system, it gives voters a dual ballot with both a vote for the representative of their district and a vote for a party. Also like a parallel system, it creates a legislature that combines single member district seats with additional seats.

However, while in a parallel system the district and list portions of the election are essentially independent from each other, MMP attempts to use the additional seats to compensate for any disproportionalities created in the district elections. Let’s apply the idea to example 17:

List Vote District Seats Won Adjustment Seats Allocated Total Seats

A 40% 26 14 40

B 30% 18 12 30

C 20% 4 16 20

D 10% 2 8 10

In MMP, the additional seats are often called adjustment seats. They are allocated so that the total number of seats held by a party is proportional to its share of the list vote, if possible. In the case above, it is simple enough to do this.

MMP is thought to be attractive because it gives people local representatives, while still maintaining proportionality by party. However, although MMP is used by several countries, it stands on somewhat shaky theoretical ground. This shaky ground is the assumption that different members of a party are essentially equivalent and can readily be substituted for one another.

Also, MMP systems seem to invite manipulation. For example, a party could stand to gain by running a popular incumbent district candidate as an independent rather than a member of their party. That way, they may get an extra adjustment seat, plus their pseudo-independent candidate may still win their district and always vote with them anyway, in which case they have netted an extra vote for their trouble. Along the same lines, it might be profitable for a party to split into two pseudo-separate parties, one of which aims to win seats in district elections, one of which aims to win party list seats, and both of which vote together. While these knavish manipulations may be a little bit too obvious to become a major factor in practice, the fact that they seem so childishly easy is unsettling.

Some countries use systems which fall somewhere in between a parallel system and a pure MMP system. For example, rather than attempting to make proportionality exact, there could be a limit to the degree of disproportionality allowed. For example, a rule that a party's percentage of total seats cannot be greater than their percentage of the list vote plus five percent.

III. Direct democracy systems

When we take proportional representation to its logical extreme, we come to direct democracy. The proportionality of a PR system becomes more complete as the number of representatives grows. As long as the number of representatives is greater than the number of voters, then representation is always to some degree an approximation, a simplification of the electorate. However, as the number of representatives approaches the number of voters, representation approaches perfection. When the set of representatives is identical to the set of voters, then representation is absolute.

Direct democracy is the ideal that every member of a group (for example, a nation) should have the opportunity to have a vote in every decision that the group makes, rather than only having the power to vote for a representative.

However, while direct democracy seems to be an essential part of democracy itself, it is challenging to apply it on a large scale. It seems dishonest to call any government fully democratic that does not use direct democracy, and yet it is difficult to imagine that every citizen of a large state would be able to come to a fully informed decision on every piece of public policy that would make it to a legislature. Or, if they were able to do so, it is hard to imagine that they would have time to do much else. The concern is that public decisions would be somewhat arbitrary, and possibly that voters' lack of complete knowledge could be severely taken advantage of by those who could afford the services of public relations firms.

III.A. Proxy systems

Note: For a much more recent take on proxy systems, please see my working paper on direct democracy by delegable proxy.

III.A.1. Basic proxy system

Perhaps the best way to cope with this problem is to develop a proxy system. The basic idea of this is that voters have the option of designating a proxy to carry the weight of their vote in deciding an issue. Voters should be able to change their proxies at will, and there should be no minimum threshold of votes needed for anyone to serve as a proxy. The value of a proxy system is that even if people do not have time to become fully educated on the issues, then they may know of someone who does, someone with whom they share common values and beliefs.

III.A.2. Possible additions to proxy system

Below are some possible rules that might make a proxy system more attractive.

III.A.2.a. Proxy system with optional direct vote

As a voter I can choose from issue to issue whether to vote directly on that issue or to defer to their proxy. This is important because it preserves people's ability to express their opinion directly when they have one, while still maintaining the benefits of the proxy system.

III.A.2.b. Proxies of proxies

If I indicate someone as my proxy, and she indicates someone as her proxy, then the weight of my vote will be passed along to her proxy. And perhaps to her proxy's proxy, and so on. This will prevent votes from being wasted, and allow the accumulation of votes to people who are trusted by people who are in turn trusted by others.

III.A.2.c. Ranked proxy lists

I can have a ranked list of standing proxies (rather than only a single proxy), so that if my first proxy neither shows up for the vote nor has a standing proxy of her own, then the weight of my vote instead is transferred to my second proxy. And so on. This is another mechanism to prevent votes from being wasted.

III.A.2.d. Issue-specific proxies

On any given issue I also have the option of indicating a proxy or list of proxies different from my standing list, just to receive the weight of my vote for that one issue. One reason this might be good is that it would allow voters to indicate as proxies people who are knowledgeable in the field that a specific issue relates to. For example, if the issue is relevant to ecology, then a voter might indicate an ecologist as their proxy for that issue, or a staff member at an NGO that deals with the environment. Or, rather than being a matter of a field of study, a voter may delegate his vote to someone whom he knows has educated themselves well about that issue in particular. For example, if the issue is choosing between different versions of a trade bill and the voter knows someone who has read all of the different versions personally. Even if most voters would not know such a person, their proxies and their proxies' proxies might.

III.A.2.e. Summary of proxy rules

Taking these ideas together, each voter has 3 options when faced with a given issue:

1. Specifically vote on the issue. (This could include formally abstaining.)

2. Indicate a specific proxy or ranked list of proxies, other than those indicated on their standing list, just for the purpose of their vote on the issue.

3. Do nothing, in which case their voting power goes in the direction indicated by their standing proxy list (assuming that they have such a list on file).

III.A.2.f. Resolving paradoxes

If a voter indicates a new proxy list specifically for an issue, the effect for that issue should be the same as if that list had been their standing proxy list and they had indicated it by default. In either case, a proxy list is indicated.

It is possible that a paradox might arise, if for example voter A indicates B as his first proxy, B indicates C as his first proxy, and C indicates A as his first proxy. One possible rule to resolve this paradox is as follows: "A vote shouldn't travel the same proxy path twice."

Given the above case, A's vote has traveled the path A-->B, then the path B-->C, and then the path C-->A. Therefore, according to this rule, once A's vote returns to A, it should not once again travel the path from A to B. Instead, it should travel to the next proxy as ranked on A's proxy list.

The proxy path rule is not very important, since such paradoxes are not especially hairy. Other rules are possible, for example "a vote shouldn't be assigned to the same person twice," in which case A's vote would be transferred to C's second proxy rather than being assigned to A once again.[*]

III.A.3. Voting systems to be used, and relation to other governmental structures

As for the voting method used to decide the actual issues given a proxy system, that is left open. When majority rule is appropriate, Smith-efficient methods are attractive. For issues where proportional representation is appropriate, STV or CPO-STV are attractive. Other methods might be attractive given different circumstances.

Such a proxy system would not necessarily make elected representatives unnecessary. I think that it would be more practical for it to serve as a complement to rather than a replacement for representative government.

Indeed, the legal bindingness of such a direct vote is left open as well, that is, whether it creates law in itself, whether it is subject to amendments revisions, vetoes, and if so by whom, etc. There might be many situations where it would be attractive to have a direct vote, but have it not be legally binding. That is, where the citizens are able to express their opinions actively (rather than through randomly sampled polls, etc.), but where the final decision is left to the traditional structures of government.

Actually, this non-binding vote might be the best place to start from in terms of building a direct democracy from a representative democracy, so that public participation and trust can be developed before legal power is invested in it.

III.A.4. Medium of communication and frequency of direct votes

With any direct democracy system, one of the biggest questions is regarding the medium of communication that would support it.

The internet is one intuitive choice, but there is an issue of security, that is the possibility that someone might be able to hack into the system and change the outcome of the vote. Also, there is an issue of access, that is the fact that not everyone has equal access to the internet.

Another possibility is to use traditional voting stations, such as the ones that are set up on election days (although it may be preferable to use computerized voting machines, etc.). The data from each station can then be physically carried (perhaps in some digital format) from each station to some central location for the tally, or transmitted by some other kind of secure channel.

The frequency with which these stations could be set up and used depends on the amount of resources that a given society is willing to spend on direct democracy, in relation with the desire for frequency of public votes. For example, it might be costly (although not impossible) to have stations running on a permanent basis, and hence to have a kind of pure direct democracy where every issue passing through the legislature is subject to a direct vote.

Alternately, one might consider setting up stations for something like four or five direct democracy votes per year, and to cram each voting day with a bunch of issues which can be discussed in the weeks and months leading up to them. There might be situations where emergency direct votes can be called ahead of schedule. For example, if a nation was considering launching an offensive war, it might be desirable to require majority approval in a direct vote in order to proceed.

Given a few direct votes per year, although the popular vote wouldn't be the sole determinant of policy, it could have a very significant impact on policy, and the citizens of a nation would have a very substantial opportunity to express their will directly, rather than in terms of favoring one representative over another.

Again, for further details on proxy voting, please click here.

[*] Mueller 1, p.271

[*] LeGrand 1

[*] Condorcet 1

[*] There is a bewlidering variety of names for this most basic of Condorcet methods. The term “minimax” is used by Rob Loring, and Steve Eppley (the latter specifically to describe the winning votes version), the term "maximin" is used by Tideman, the term “plain Condorcet” is used by Ossipoff, the term “successive reversal” is used by Nurmi, and the term “Simpson” is used by LeGrand.

[*] Smith 1

[*] Tideman 3, p.176

[*] Ossipoff 2

[*] Tideman 3, p.171

[*] Schulze 2

[*] Tideman 3, p.175

[*] Tideman 3, p.222

[*] LeGrand 1

[*] Nurmi 1

[*] Cretney 1

[*] Ossipoff 1

[*] LeGrand 2

[*] Mueller 1, p.147

[*] LeGrand 1

[*] Ossipoff and Paielli 1

[*] Lijphart 1, appendix

[*] Tideman 3, p.267

[*] Lijphart 1, appendix

[*] Tideman 1, and Tideman 3, p.270

[*] This method is defined in Tideman 1, and in Tideman 3 on p.278

[*] For more details, see Green-Armytage 2

[*] Green-Armytage 3

[*] As far as I know, the ideas in sections III.A.2.c., III.A.2.d., III.A.2.e., and III.A.2.f. are original to Green-Armytage 1.

[*] Invented by James Green-Armytage, June 8, 2004. First proposal is Green-Armytage 4. Current proposal is Green-Armytage 5.